數學實驗:畫鉛垂線,找交點:對下列各關係 \(\displaystyle{\left( x,y \right) }\) 的圖像,畫任意一條鉛垂線 (即垂直於 \(\displaystyle{ x }\) 軸、平行於 \(\displaystyle{ y }\) 軸的直線),看看能否找到一條鉛垂線,與圖像的交點多於一個。
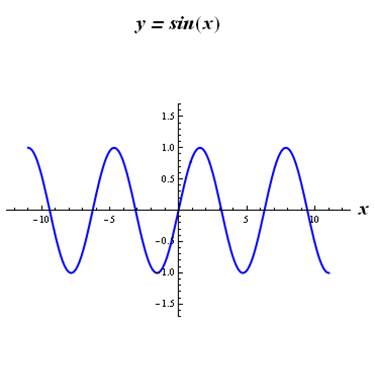
(1) 關係 \(\displaystyle{y=\sin \left( x \right) }\)
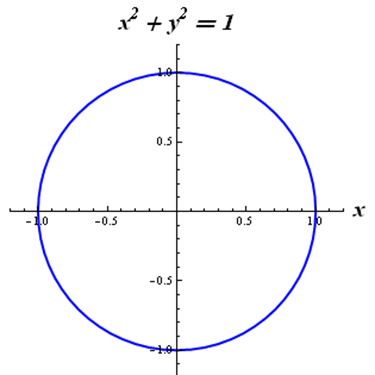
(2) 關係 \(\displaystyle{{{x}^{2}}+{{y}^{2}}=1 }\)
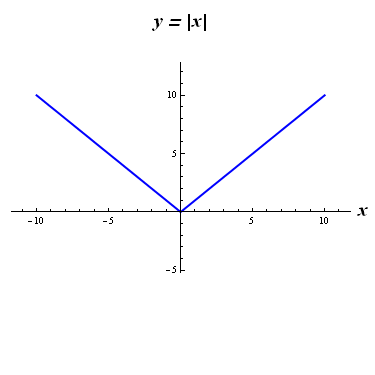
(3) 關係 \(\displaystyle{y=\left| x \right| }\)
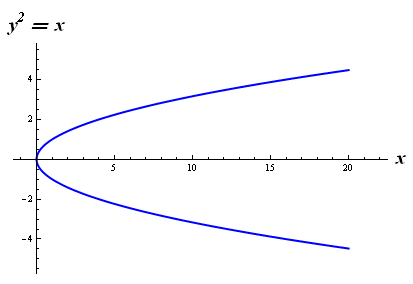
(4) 關係 \(\displaystyle{{{y}^{2}}=x }\)
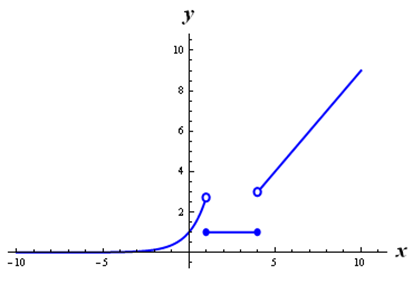
(5) 關係 \(\displaystyle{ y=\left\{ \begin{align} {{e}^{x}} & \quad x\lt 1 \\ 1 & \quad 1\le x\le 4 \\ x-1 & \quad x \gt 4 \end{align} \right.}\)
實驗提問:
1. 找出各個關係的圖像與鉛垂線的交點的個數。
| 關 係 | 答 案 | 選項 (交點的個數) |
|---|---|---|
| (1) 關係 \(\displaystyle{y=\sin \left( x \right) }\) |
(A) \(\displaystyle{ 0 }\) 个 (B) \(\displaystyle{ 0\sim 1 }\) 个 (C) \(\displaystyle{ 1 }\) 个 (D) \(\displaystyle{ 0\sim 2 }\) 个 (E) \(\displaystyle{ 2 }\) 个 (F) \(\displaystyle{ 0\sim N }\) \(\displaystyle{\left( N \gt 2 \right) }\) |
|
| (2) 關係 \(\displaystyle{{{x}^{2}}+{{y}^{2}}=1 }\) | ||
| (3) 關係 \(\displaystyle{y=\left| x \right| }\) | ||
| (4) 關係 \(\displaystyle{{{y}^{2}}=x }\) | ||
| (5) 關係 \(\displaystyle{ y=\left\{ \begin{align} {{e}^{x}} & \quad x\lt 1 \\ 1 & \quad 1\le x\le 4 \\ x-1 & \quad x \gt 4 \end{align} \right.}\) |
2. 如果存在一條鉛垂線,與該關係圖像的交點多於一個,這些交點的坐標 \(\displaystyle{\left( x,y \right) }\) 有甚麼特點?
A. 這些交點的坐標 \(\displaystyle{\left( x,y \right) }\) 的 \(\displaystyle{ x }\) 和 \(\displaystyle{ y }\) 都相等
B. 這些交點的坐標 \(\displaystyle{\left( x,y \right) }\) 的 \(\displaystyle{ x }\) 都相等,但 \(\displaystyle{ y }\) 都不相等
C. 這些交點的坐標 \(\displaystyle{\left( x,y \right) }\) 的 \(\displaystyle{ y }\) 的值都相等,但 \(\displaystyle{ x }\) 的值不相等
D. 這些交點的坐標 \(\displaystyle{\left( x,y \right) }\) 的 \(\displaystyle{ x }\) 和 \(\displaystyle{ y }\) 都不相等
3. 根據第 2 題的結果,判定哪些關係是函數,哪些不是函數?
| 關 係 | 是 函 数 ? |
|---|---|
| (1) 關係 \(\displaystyle{y=\sin \left( x \right) }\) |
是 否 |
| (2) 關係 \(\displaystyle{{{x}^{2}}+{{y}^{2}}=1 }\) |
是 否 |
| (3) 關係 \(\displaystyle{y=\left| x \right| }\) |
是 否 |
| (4) 關係 \(\displaystyle{{{y}^{2}}=x }\) |
是 否 |
| (5) 關係 \(\displaystyle{ y=\left\{ \begin{align} {{e}^{x}} & \quad x\lt 1 \\ 1 & \quad 1\le x\le 4 \\ x-1 & \quad x \gt 4 \end{align} \right.}\) |
是 否 |
圖像 \(2\) 與圖像 \(4\) 中,存在一條鉛垂線與該關係圖像的交點多於一個,即存在兩個不同的有序對 \(\displaystyle{\left( x,y \right) }\) 的第一個變量 \(\displaystyle{ x}\) 相同之情況,因此圖像 \(2\) 和圖像 \(4\) 表示的關係不是函數關係。而其他三個關係的圖像,與任何一條鉛垂線最多交於一點,表示不存在兩個不同的有序對 \(\displaystyle{\left( x,y \right) }\),其第一個變數 \(\displaystyle{ x }\) 相同的情況,即該關係的定義域上的每個元素 \(\displaystyle{ x }\) 都準確對應於其值域上的唯一一個元素 \(\displaystyle{ y }\),可見他們是函數關係。
圖像 \(5\) 表示的函數叫分段函數,該類函數在 \(\displaystyle{ x }\) 的不同定義區間內之表達式不相同,描繪這類函數的圖像時,用實心圓點表示包含該端點,用空心圓點表示不包含該端點。
垂直線測試法 (vertical line test) 判定某關係是否為函數:將關係 \(\displaystyle{\left( x,y \right) }\) 的圖像繪製在直角坐標系中,如果任何一條鉛垂線,即垂直於 \(\displaystyle{ x }\) 軸的直線,與關係的圖像不相交或只相交於一點,則該關係表示的是 \(\displaystyle{ y }\) 是 \(\displaystyle{ x }\) 的函數。
例如,數學實驗中,圖像 \(1\)、\(3\)、\(5\) 表示的關係是函數,而圖像 \(2\) 和 \(4\) 不是函數。