實例:在生活中,常常需要將同一性質的不同單位之間進行數值換算,如在市場和超市中常看到兩種不同的重量單位:千克和磅。\(\displaystyle{ 1 }\) 千克大約等於 \(\displaystyle{ 2.205 }\) 磅。兩種單位之間是一對一的關係,也就是說磅數是千克數的函數,千克數也是磅數的函數。如果用 \(\displaystyle{ x }\) 表示千克數,\(\displaystyle{ y }\) 表示磅數,那麼如何表示這個函數呢?
以下就以此實例介紹幾種函數的表達方式。
把函數的一些自變量和應變量的值對應地列出。
根據千克和榜的換算關係,填寫下表:
| 千克數 \(\displaystyle{ x }\) | \(10\) | \(20\) | \(31\) | \(44\) | \(57\) | \(70\) |
| 磅數 \(\displaystyle{ y }\) |
| 千克數 \(\displaystyle{ x }\) | \(10\) | \(20\) | \(31\) | \(44\) | \(57\) | \(70\) |
| 磅數 \(\displaystyle{ y }\) | \(22.05\) | \(44.1\) | \(68.255\) | \(97.02\) | \(125.685\) | \(154.35\) |
這就是列表法表示的函數。習慣上把自變量 \(\displaystyle{ x }\) 放在第一行,應變量 \(\displaystyle{ y }\) 放在第二行。
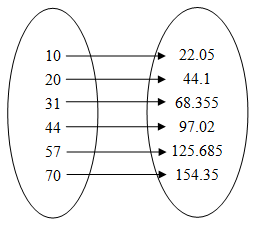
將每個自變量的值與其應變量的值以箭咀相連來表達函數。
以列表法中的數據為例,用映射圖法表示如下:
思考:列表法和映射圖法表示方法類似,他們有甚麼優點和缺點呢?
優點:直接易明。
缺點:需要將自變量和應變量的值一一列出,較繁瑣。
運用公式 \(\displaystyle{y=2.205x }\) 可將任意一個千克數 \(\displaystyle{ x }\) 表示成磅數 \(\displaystyle{ y }\),這種函數的表達方式稱為代數法。
優點:不需要全列出自變量和應變量的值,較簡潔。
缺點:沒有列表法和映射圖法直接。
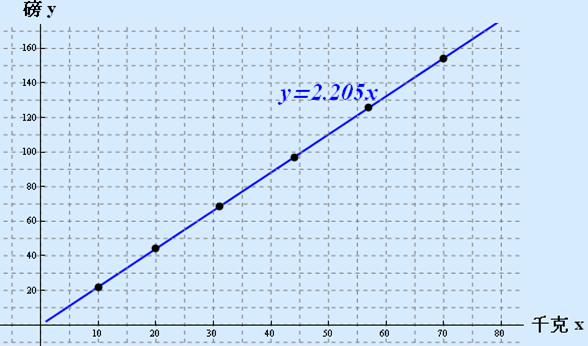
在直角坐標平面中,函數可以由其所有有序對 \(\displaystyle{\left( x,y \right) }\) 所代表的點組成的圖像表示出來。每個有序對的 \(\displaystyle{ x }\) 值對應於點的橫坐標,\(\displaystyle{ y }\) 值對應於點的縱坐標。根據公式 \(\displaystyle{ y=2.205x }\),任何一個定義域中是千克數 \(\displaystyle{ x }\),都有對應的磅數 \(\displaystyle{ y }\),因此用線段將各點連接起來,此函數的圖像是一條連續的直線。
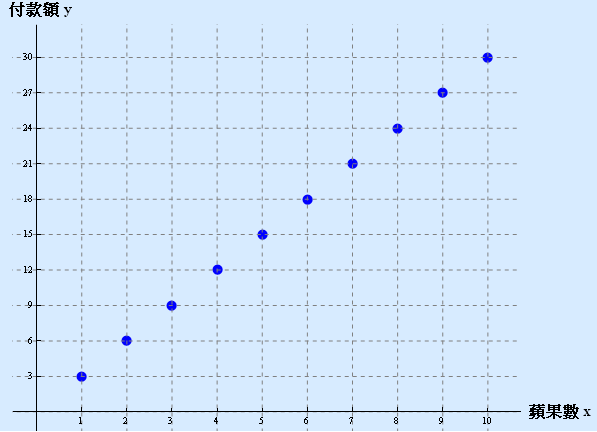
注意:並不是所有的函數的圖像都可以將各點用線 (直線或曲線) 相連,如到超市買蘋果,一個蘋果 \(\displaystyle{ 3 }\) 元,那麼蘋果的個數 \(\displaystyle{ x }\) 與付款額 \(\displaystyle{ y }\) 的函數關係就是 \(\displaystyle{ y=3x }\),用圖像法表示就是由許多個點組成,點之間沒有線連接,如圖所示,因為蘋果只能整個買,所以蘋果的個數 \(\displaystyle{ x }\) 的定義域是自然數,即 \(\displaystyle{ 1,2,3\ldots \ldots }\) 當 \(\displaystyle{ x }\) 為非自然數時,如 \(\displaystyle{ x=1.3 }\),在圖像中沒有與之對應的點。
除了用 \(\displaystyle{ y }\) 表示 \(\displaystyle{ x }\) 的函數外,通常還會用一些其他特別的記號,例如 \(\displaystyle{f\left( x \right) }\)、\(\displaystyle{ F\left( x \right) }\)、\(\displaystyle{ g\left( x \right) }\)、\(\displaystyle{ h\left( x \right) }\) 等來表示 \(\displaystyle{ x}\) 的函數,最常用的是記號 \(\displaystyle{ f \left( x \right) }\)。
例如,函數 \(\displaystyle{ y =7x+4 }\) 可寫成 \(\displaystyle{ f\left( x \right) =7x+4 }\)。
讀作 \(\displaystyle{''fx'' }\) 或 \(\displaystyle{''x }\) 的函數 \(\displaystyle{f'' }\),表示在 \(\displaystyle{ x }\) 處函數 \(\displaystyle{ f }\) 的值。
當 \(\displaystyle{ x=a }\) 時,函數值表示為 \(\displaystyle{f\left( a \right) }\),即將 \(\displaystyle{ x=a }\) 代入函數 \(\displaystyle{f\left( x \right) }\) 的表達式中得到函數的值。這樣可以簡潔地表達函數值 (應變量) 與自變量的關係。
例如,函數 \(\displaystyle{f\left( x \right)=7x+4 }\),那麼 \(\displaystyle{f\left( -2 \right)=7\times \left( -2 \right)+4=-10 }\)。
函數 \(\displaystyle{f\left( x \right) }\) 還表示了定義域 X 與值域 Y 之間的映射關係,可以寫成 \(\displaystyle{f:X\to Y }\)。
例如,函數 \(\displaystyle{f\left( x \right)=7x+4 }\) 也可以表示為 \(\displaystyle{f:x\to 7x+4 }\)。
注意:除了可以用不同的符號表示函數,也可以用不同的符號作為函數的自變量,函數關係不變。
例如:\(\displaystyle{f\left( x \right)=7x+4 }\)、\(\displaystyle{f\left( t \right)=7t+4 }\)、\(\displaystyle{ f\left( u \right)=7u+4 }\) 都表示同一個關係。