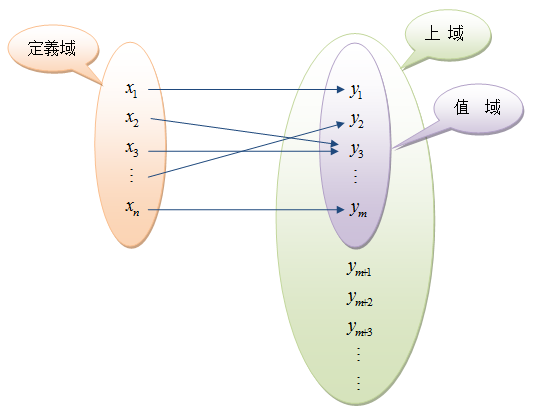
定義域 (domain):函數的自變量 \(\displaystyle{ x }\) 所有可取值構成的整體。\(\displaystyle{ x }\) 的取值範圍不可以超出定義域的範圍。
值域 (range):對應於定義域範圍內的自變量 \(\displaystyle{ x }\),函數的應變量 \(\displaystyle{ y }\) 所有可取值的範圍。定義域上的每個元素都準確對應於其值域上的唯一一個元素。值域範圍依賴於函數的定義域範圍。
上域 (co-domain):函數的應變量 \(\displaystyle{ y }\) 的考慮範圍。它是一個必須包含值域的整體,上域比值域的範圍大或正好相同。
例如:函數 \(\displaystyle{ y=ax+b }\) (\(\displaystyle{ a,b }\) 為實數,\(\displaystyle{a\ne 0 }\)) 的定義域和值域都是所有實數;函數 \(\displaystyle{y=\sqrt{x} }\) 的定義域為所有非負實數 (負數沒有平方根),值域也是所有非負實數;函數 \(\displaystyle{y=\frac{1}{x-a} }\) (\(\displaystyle{ a }\) 為實數) 的定義域為 \(\displaystyle{ a }\) 以外的所有實數 (除數不為零),值域為非零的所有實數。
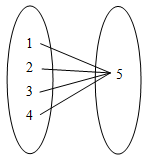
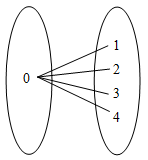
下列各圖代表 \(\displaystyle{ x }\) 與 \(\displaystyle{ y }\) 的關係。試判斷 \(\displaystyle{ y }\) 是不是 \(\displaystyle{ x }\) 的函數。如果是,寫出其定義域、值域和上域。
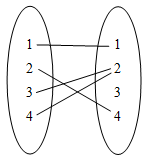 |
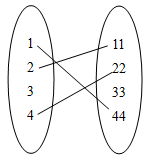 |
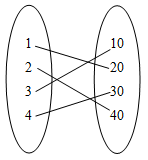 |
 |
 |
| \(\displaystyle{ x }\) 與 \(\displaystyle{ y }\) 的關係 | \(\displaystyle{ y }\) 是 \(\displaystyle{ x }\) 的函數嗎? | 定義域 | 值 域 | 上域 |
|---|---|---|---|---|

|
是 | \(\displaystyle{\left\{ 1,2,3,4 \right\} }\) | \(\displaystyle{\left\{ 1,2,4 \right\} }\) | \(\displaystyle{ \left\{ 1,2,3,4 \right\} }\) |

|
不是,因為定義域中的元素 「3」 沒有相對應的 \(\displaystyle{ y }\) 值 | |||

|
是 | \(\displaystyle{ \left\{ 1,2,3,4 \right\} }\) | \(\displaystyle{ \left\{ 10,20,30,40 \right\} }\) | \(\displaystyle{ \left\{ 10,20,30,40 \right\} }\) |

|
是 | \(\displaystyle{ \left\{ 1,2,3,4 \right\} }\) | \(\displaystyle{ \left\{ 5 \right\} }\) | \(\displaystyle{ \left\{ 5 \right\} }\) |

|
不是,因為定義域中的元素對應的 \(\displaystyle{ y }\) 值不唯一 |
思考:爲甚麽需要值域又需要上域呢?
值域精確描述了定義域中所有 \(\displaystyle{ x }\) 所對應的 \(\displaystyle{ y }\) 值,既不能遺漏一個 \(\displaystyle{ y }\),也不能多出一個 \(\displaystyle{ y }\);而上域可以不必這麼精確,它不能遺漏一個 \(\displaystyle{ y }\),但是可以多出一些 \(\displaystyle{ y }\)。
有些時候,精確交待應變量的範圍 (即值域) 是很麻煩或是不必要的,這時可以用一個更大的範圍 (即上域) 來描述一個函數應變量的取值範圍。