在下表中,根據國家的名稱填寫其首都,或由其首都填寫國家的名稱,完成下表的空白處:
| 國 家 | 首 都 |
|---|---|
| 中國 | 北京 |
| 美國 | 華盛頓 |
| 英國 | 倫敦 |
| 法國 | |
| 德國 | |
| 渥太華 | |
| 里斯本 | |
| 希臘 | |
| 埃及 | |
| 曼谷 |
調查一下周圍朋友的生日,找出他們的星座。
實驗提問:
每一個朋友都有對應的星座。
|
是 |
否 |
每一個朋友只對應一個星座。
|
是 |
否 |
每一個星座最多只有一個朋友對應。
|
是 |
否 |
之前所學習的全等三角形的判定條件中,不包括 \(\rm{SSA}\),即已知兩個三角形有兩對對應邊相等,而且有一對非夾角的對應角相等,不能判定這兩個三角形全等。爲甚麽呢?以下通過實驗來證實。
已知三角形 \(\displaystyle{ ABC }\),邊 \(\displaystyle{ AB =10 }\) \(\displaystyle{ \text{cm} }\),\(\displaystyle{\angle ABD={{30}^{\circ }} }\)。畫出以下幾種情況下的三角形:
先畫邊 \(\displaystyle{ AB }\),再以點 \(\displaystyle{ B }\) 為端點畫一條射線 \(\displaystyle{ BD }\),使 \(\displaystyle{\angle ABD={{30}^{\circ }} }\),最後在射線 \(\displaystyle{ BD }\) 上尋找 \(\displaystyle{ C }\) 點,使 \(\displaystyle{ AC }\) 等於相應的長度。在此,可以運用圓規,以 \(\displaystyle{ A }\) 為圓心,\(\displaystyle{ AC }\) 的長度為半徑畫圓,圓與射線 \(\displaystyle{ BD }\) 的交點即為 \(\displaystyle{ C }\) 點。
提問:(1) ~ (4) 的情況,分別可得幾個不同的三角形 \(\displaystyle{ ABC }\)。
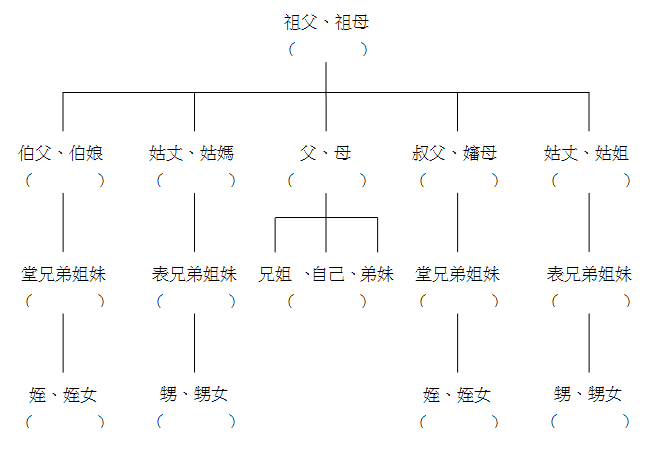
嘗試給自己的家族畫一張簡易的成員關係圖,類似於右圖的方式。如果親戚比較少,查找一些名門旺族的家譜,繪製一張含有家庭成員較多的家譜。
提問:
結論:在一個大家族中,一個人會有多個姑媽、伯父、堂兄弟姐妹,也會有多個姪 (女)。同樣,一個伯父或姑媽也會有多個兄弟姐妹、姪 (女)、甥 (女),這是多對多的關係。例如,姪和伯父之間就是一種多對多的關係。這種多對多的關係普遍存在於家族成員關係中。
關係 (relation):一組有序對組成的集合。有序對可以用 \(\displaystyle{\left( x,y \right) }\) 表示。
關係主要包括一對一、多對一、一對多、多對多這四類。
實驗 \(1\) 描述了 (國家,首都) 這種一對一的有關係;實驗 \(2\) 說明了 (生日,星座) 是一種多對一的關係;實驗 \(3\) 表示了在該種情況下,(三角形,邊長) 之間的多對一的關係;實驗 \(4\) 顯示了家族各成員之間的多對多的關係。