一般來說,描述與描繪軌跡需要注意以下兩點:
我們可利用一些工具來協助描繪軌跡。
數學實驗:現準備一枚釘子、一根長 \(\displaystyle{ 12 }\) \(\displaystyle{ \text{cm} }\) 的繩子,一枝鉛筆及一塊大的硬卡紙。 在硬卡紙的中央畫上一個固定點 \(\displaystyle{ O }\) ,假設 \(\displaystyle{ P }\) 為移動點,而它的移動特征是永遠與 \(\displaystyle{ O }\) 點保持一個固定的距離 \(\displaystyle{ 7 }\) \(\displaystyle{ \text{cm} }\)。 運用手上的工具,觀察 \(\displaystyle{ P }\) 點的移動軌跡。
實驗步驟:
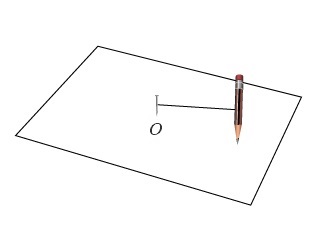
利用模擬程式,找出始終與平面上某固定點 \(\displaystyle{ O }\) 保持固定距離 \(\displaystyle{ 7 }\) \(\displaystyle{ \text{cm} }\) 的 \(\displaystyle{ P }\) 點的軌跡。
實驗方法:在模擬程式中,拖動 \(\displaystyle{ P }\) 點,當 \(\displaystyle{ P }\) 點的位置滿足實驗題目的條件時,模擬程式會自動用紅色點記錄下來。觀察滿足條件的 \(\displaystyle{ P }\) 點的軌跡,完成下列問題。
\(\displaystyle{ P }\) 點的軌跡是一個圓心為O,半徑為 \(\displaystyle{ 7 }\) \(\displaystyle{ \text{cm} }\) 的圓。
限制條件:在一個平面上,動點 \(\displaystyle{ P }\) 與一個固定點 \(\displaystyle{ O }\) 保持固定的距離 \(\displaystyle{ r }\) 。
描述:\(\displaystyle{ P }\) 點的軌跡是一個以 \(\displaystyle{ O }\) 為圓心,\(\displaystyle{ r }\) 為半徑的圓。
數學實驗:利用模擬程式,找出始終與平面上兩個固定點 \(\displaystyle{ A }\) 和 \(\displaystyle{ B }\) 保持相等距離的 \(\displaystyle{ P }\) 點的軌跡。
實驗方法:在模擬程式中,拖動 \(\displaystyle{ P }\) 點,當 \(\displaystyle{ P }\) 點的位置滿足實驗題目的條件時,模擬程式會自動用紅色點記錄下來。 觀察滿足條件的 \(\displaystyle{ P }\) 點的軌跡,完成下列問題。
動點 \(\displaystyle{ p}\) 的軌跡是線段 \(\displaystyle{ AB }\) 的垂直平分線。
限制條件:在一個平面上,動點 \(\displaystyle{ P }\) 與兩個固定點 \(\displaystyle{ A }\) 和 \(\displaystyle{ B }\) 保持相等的距離。
描述: \(\displaystyle{ P }\) 點的軌跡是線段 \(\displaystyle{ AB }\) 的垂直平分線。
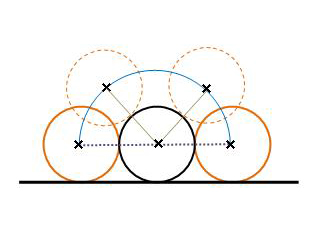
將兩個 \(10\) 元硬幣並排放在一起。現將原本在左邊的硬幣沿着右邊已固定的硬幣的周邊滾動至右邊,如圖所示。
試繪畫并描述滚動硬幣的圓心在這個過程中所行經的路線。
開始時,這兩個硬幣的 "\(10\)" 字都是直立。當原本在左邊的硬幣滾動至右邊時,它的 "\(10\)" 字是直立或是倒立?

行經的路線是以已固定的硬幣的圓心為圓心的半圓周,而它的半徑是硬幣的半徑的兩倍。
如動畫所示,當原本在左邊的硬幣滾動至右邊時,它的 "\(10\)" 字還是直立的。