在上一節,我們介紹了分佈域,它是一個簡單的離差量度。不過,分佈域容易受極端數據影響,所以我們希望找一個沒那麼容易受極端數據影響的離差量度。四分位數間距(interquartile range)就是一個這樣的量度。
簡單來說,四分位數間距就是數據組中,正中間那一半數據的分佈域。基於數據是否分組,四分位數間距的計算方法有所不同。
我們知道,若把不分組數據從小至大排列,則中位數會把該組數據劃分成上下兩等份(若數據的數目為單數,則上下兩部分都不包括中位數)。同理,四分位數會把該組數據劃分成四等分,即
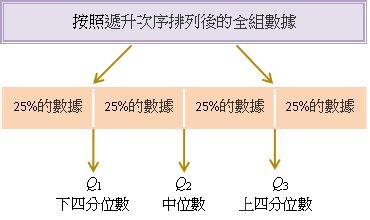
一組數據有三個四分位數,包括
四分位數間距就是上四分位數和下四分位數之差,即
(以下答案僅供參考,任何言之成理的答案均可接受。)
我們在兩部分所得的結論並不一致。由於\(\;S_1\;\)包括一個極端數據\(\;100\),所以其分佈域較大,但撇除極端數據後,\(\;S_2\;\)的離散程度就較\(\;S_1\;\)高,所以\(\;S_2\;\)的四分位數間距比\(\;S_1\;\)的大。
下表為某班\(\;40\;\)名學生在一次考試中的成績,求它的四分位數間距。
首先把這組數據從小至大排列:
它的四分位數間距為 \[ \hbox{四分位數間距} = \frac{67+69}{2} - \frac{44+42}{2} = 68 - 43 = 25 \]我們可以利用分組數據的累積頻數多邊形(或累積頻數曲線)來讀出該組數據的四分位數,其中
跟不分組數據的情況相同,四分位數間距就是上四分位數和下四分位數之差,即
注意
若把不分組數據的例子二中之數據分組,可得下表:
要找出它的四分位數間距,我們先繪畫它的累積頻數多邊形。
數據總數為\(\;40\),在累積頻數多邊形中,\(y=30\;\)對應\(\;x=68.25\),而\(\;y=10\;\)對應\(\;x=41.5\)。所以,這組數據的四分位數間距為 \[ \hbox{四分位數間距} = 68.25 - 41.5 = 26.75 \]
注意 比較不分組數據的例子二和這裡的結果,可見把數據分組會影響它的四分位數間距。
由於分佈域和四分位數間距都是以數據組中的幾項數據來計算,並沒有把所有數據都納入考慮範圍,因此以這兩種方法來量度離差有其不足之處。以下讓我們來探討一下它們的不足。
考慮數據組 \begin{align*} S_1 &= \{ 1,2,3,4,5,5,6,7,8,9 \} \\ S_2 &= \{ 1,3,3,5,5,5,5,7,7,9 \} \end{align*}
已知\(\;S_1\;\)和\(\;S_2\;\)的集中趨勢相同,我們考慮兩組數據的離差。
試完成下表。
| \(S_1\) | \(S_2\) | |
|---|---|---|
| 最小值 | ||
| 下四分位數 | ||
| 中位數 | ||
| 上四分位數 | ||
| 最大值 | ||
| 分佈域 | ||
| 四分位數間距 |