1. 首頁
  2. 數學學習模組
  3. 二次方程的求解
  4. 第一課 以因式法解二次方程
繁 简
第二節 因式法解二次方程
因式分解二次函數 —— 數學實驗

因式分解二次函數的目標


把 \(ax^2 + bx + c\) 寫成 \( (px - r)(qx -s) \) 的形式。

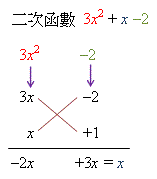
例如： 以因式分解 \(3x^2 + x - 2\)，可得

\(\qquad \qquad 3x^2 + x - 2 = (3x - 2)(x + 1) \)


請在互動活動試以因式分解 \(2x^2 - 3x - 14\)。

互動活動

跟進學習

剛學習了因式分解二次函數，現請完成以下表。

注：請把 \(x\) 最大的係數（正數）的因子放在前面的因式。

例如將 \(3x^2 + x - 2 \) 寫為 (3\(x - 2)(x + 1)\) 而不是

\(\qquad (x + 1)(\)3\(x - 2) \,\) 或 \(\,\)(-3\(x + 2)(-x - 1)\)。

二次函數 因式分解
\(2x^2 - 5x + 3 \) (
  • 1
  • 2
 \(x\) +
  • -3
  • -1
  • 1
  • 3
 )
(
  • 1
  • 2
 \(x\) +
  • -3
  • -1
  • 1
  • 3
 )
\(3x^2 + 7x - 6\) (
  • 1
  • 3
 \(x\) +
  • -6
  • -3
  • -2
  • -1
  • 1
  • 2
  • 3
  • 6
 )
(
  • 1
  • 3
 \(x\) +
  • -6
  • -3
  • -2
  • -1
  • 1
  • 2
  • 3
  • 6
 )
\(9x^2 - 5x - 4 \) (
  • 1
  • 3
  • 9
 \(x\) +
  • -4
  • -2
  • -1
  • 1
  • 2
  • 4
 )
(
  • 1
  • 3
  • 9
 \(x\) +
  • -4
  • -2
  • -1
  • 1
  • 2
  • 4
 )


因式分解二次函數

我們剛學習過以因式分解二次函數 \(ax^2 + bc + c\)，其中 \(a \ne 0\)。

我們可以利用因式法來解二次方程。此方法是根據以下的公理而得：


對於任意兩個實數 \(a\) 與 \(b\)，若 \(ab = 0\)，則 \(a = 0\) 或 \(b = 0\)。

以上面的互動活動為例，我們可以將 \(2x^2 - 3x - 14\) 因式分解為 \((2x - 7)(x + 2)\)。

因此，若相對的二次方程為 \(2x^2 - 3x - 14 = 0\)，則

        \((2x - 7)(x + 2) = 0 \, \ \) 
\(2x - 7 = 0 \, \ \)    或    \(x + 2 = 0 \, \)   
\(x = \displaystyle{\frac{7}{2}}\)    或    \(x = -2\)

因此，\(2x^2 - 3x - 14 = 0\) 的根是 \(x = \displaystyle{\frac{7}{2}}\) 和 \(-2\)。

上一節
返回