在這一節中,我們將會以數學實驗來探索圓內接四邊形的對角的關係。
在右面的模擬模型, \(A\)、\(B\)、\(C\) 與 \(D\) 點是在圓周上預設的位置。
請使用模擬模型自動量度各圓內接四邊形的角的結果,並在以下列表的空格上填上適當的答案。
| \(\angle DAB (^{\circ})\) | \(\angle ABC (^{\circ})\) | \(\angle BCD (^{\circ})\) | \(\angle CDA (^{\circ})\) |
| \(69\) |
根據列表所得,請填上圓內接四邊形每組對角之和。
| \(\angle DAB + \angle BCD (^{\circ})\) | \(\angle ABC +\angle CDA (^{\circ})\) |
在模擬模型中,請沿着圓周滑動 \(B\)、\(C\) 和 \(D\) 點而形成另一個圓內接四邊形 \(AXYZ\)。
請在以下列表的空格上填上適當的答案。
| \(\angle ZAX (^{\circ})\) | \(\angle AXY (^{\circ})\) | \(\angle XYZ (^{\circ})\) | \(\angle YZA (^{\circ})\) |
| \(97\) |
根據列表所得,請填上圓內接四邊形每組對角之和。
| \(\angle ZAX + \angle XYZ (^{\circ})\) | \(\angle AXY +\angle YZA (^{\circ})\) |
比較這兩個活動的結果,你有否發覺每組圓內接四邊形對角之和有什麼相同之處?
我們在下一課件將會詳細地討論這特性。
從上一節的數學實驗中,我們探索到任何圓內接四邊形中,每組對角之和是 \(180^{\circ}\)。
我們可以下兩個定理來描述這屬性。
|
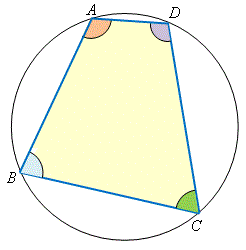
定理 18——圓內接四邊形對角 圓內接四邊形的對角互補。 即,\(\angle DAB + \angle BCD = 180^{\circ}\; ,\) 及\(\angle ABC + \angle CDA = 180^{\circ}\; 。\) |
|
定理 \(18\) 的證明:
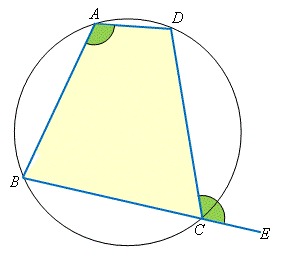
圖右為一個圓內接四邊形 \(ABCD\),而 \(BC\) 延長至圓外的一點 \(E\)。\(\angle DCE\) 稱為圓內接四邊形的一個外角,而 \(\angle DAB\) 則稱為 \(\angle DCE\) 的內對角。
從圖中,我們看到 \(\angle BCD\) 和 \(\angle DCE\) 是一對補角。因此,我們可以得到以下的定理。
|
定理 19——圓內接四邊形外角 圓內接四邊形的外角與其內對角是相等。 即,\(\angle DCE = \angle DAB \) |

|
定理 \(19\) 的證明: