已知等差數列 \(4, 9, 14, 19, \dots\),求
請在空位中填上適當的答案。
\(T_1 = \)
\(d = \)
\(S_n = \displaystyle{\frac{n}{2}}(T_1 + T_n)\)
\(S_n = \displaystyle{\frac{n}{2}}[2T_1 + (n - 1)d]\)
在題目提供的資料中沒有末項 \(T_n\) 的值。
現有等差數列的首項 \(T_1\)、項數及 \(d\)。
\(n = \)
| \(S_n \) | = |
|
\([2 \times \) \(+ (\) \(- 1) \times\) \(]\) | ||
| = | 。 |
\(S_{25} = \)
一個演奏廳內有若干排座椅。已知第一排有 \(12\) 張座椅,而其後每一排的座椅數目較前一排多 \(3\) 張。若最後一排的座椅數目是第一排的 \(6\) 倍,求演奏廳內
請在空位中填上適當的答案。
巳知在演奏廳內,每一排的座椅數目較前一排多 \(3\) 張。
該等差數列的首項(第一排)有 \(12\) 張座椅,而公差是 \(3\)。
座椅數目
首項
第二項
第三項
\(\vdots\)
第 \(n\) 項 \(n + \)
從題目及 \(a.\) 所得,
首項 \(= 12\) 項,
末項 \(= 6 \times 12 = 72\) 項,
項數 \(n = 21。\)
\(\begin{align*}\therefore {\kern 10pt} \text{座椅的總數} &= \frac{n}{2} \text{(首項 + 末項)} \\ &= \frac{21}{2} (12 + 72) \\ &= 882 \end{align*}\)
\( \therefore {\kern 10pt}\)座椅的總數是 \(882。\)
在題目提供的資料中沒有末項 \(T_n\) (即 \(l\)) 的值。
\(T_1 = \)
\(T_2 = \)
\(d = \)
\(d = T_2 - T_1\)。
| \(S_n \) | = |
|
\([2 \times \) \(+ (\) \(- 1) \times\) \(]\) | ||
| = | 。 |
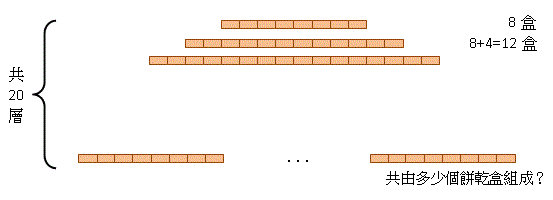
在一個食物展覽會中,某餅乾製造商展出一個由 \(20\) 層的餅乾盒疊成的展品,其中每層的餅乾盒的數目均較其上一層多 \(4\) 盒。若最高的一層有 \(8\) 個餅乾盒,問該展品是由多少個餅乾盒組成?
\(\because\)每層的餅乾盒數目均較其上一層多 \(4\) 盒。
\(\therefore\)從最高的一層計一起,每層的餅乾盒數目組成一個等差數列。
該等差數列的公差是 \(4\)。
最高的第一層 \(n = 1\) \(8\) 盒,
最底的第一層 \(n = 20\) 盒。
公式: \(T_n = T_1 + (n - 1)d\)
\(\therefore\)從最高的一層計一起,每層的餅乾盒數目組成一個等差數列。
該等差數列的公差是 \(4\)。
\(\therefore\)共需餅乾盒 盒。
公式: \(S_n = \displaystyle{\frac{n}{2}}(T_1 + T_n)\)