在日常生活中，我們常常用質量來描述物體所含物質的多少，如 \(100 \text{ g}\) 食鹽。然而，物質是由粒子構成的，例如，食鹽是由鈉離子和氯離子構成的。那麼，\(100 \text{ g}\) 食鹽是由多少個鈉離子和氯離子構成的呢？我們需要一個「橋樑」，從而將宏觀世界中物質的質量，與微觀世界中構成物質的粒子數定量地聯繫在一起。這個橋樑就是「摩爾」。

摩爾是人為定義的一個關於「物質的量」的單位。與「相對原子質量」一樣，摩爾亦是以碳–12 原子作為基準的。摩爾 (符號為 \(\text{mol}\)) 的定義如下：

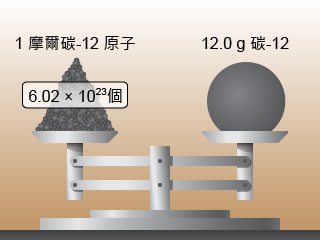
\(1 \text{ mol}\) 任何純物質 (或物種) 所含化學式單位的數目與 \(12.0 \text{ g}\) 碳–12 所含的原子數目相等。

經測定，\(12.0 \text{ g}\) 碳–12 中，約含有 \(6.02 \times 10^{23}\) 個碳–12 原子。因此，\(1 \text{ mol}\) 任何純物質 (或物種) 所含化學式單位的數目是 \(6.02 \times 10^{23}\) 個。

\(6.02 \times 10^{23}\) 是一個固定的數值，它被稱作亞佛加德羅常數 (Avogadro's constant)，符號是 \(L\)。即

\[L = 6.02 \times 10^{23} \text{ mol}^{-1}\]

亞佛加德羅常數是一個極其龐大的數字。若你有 \(1 \text{ mol}\) \(1\) 元硬幣 (即 \(6.02 \times 10^{23}\) 個 \(1\) 元硬幣)，且你每秒鐘消費 \(1\) 億元，你能估算出：這些硬幣夠你消費多少年麽？答案是：超過 \(1.9\) 億年！

摩爾是一個數量的單位。或者我們通過以下類比，來幫助你理解。

在包裝雞蛋時，人們常用「打」作為的單位。一打就是 \(12\) 個。類似地，如果有人說他買了一打書，即是說他買了 \(12\) 本書；如果有人說他有一打襯衫，即是說他有 \(12\) 件襯衫。

摩爾的概念與此十分類似，即 \(1 \text{ mol}\) 就是 \(6.02 \times 10^{23}\) 個。因此，若有人說他要購買 \(1 \text{ mol}\) 雞蛋，即是說他要購買 \(6.02 \times 10^{23}\) 個雞蛋。當然，這幾乎是不可能的。