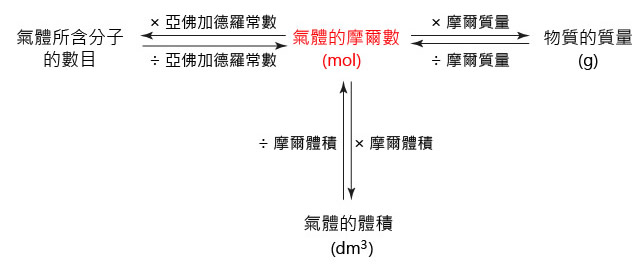
至此,藉由摩爾數 \(n\),我們能夠完成氣體所含的分子數目 \(N\) 、氣體的質量 \(m\) 和氣體的體積 \(V\) 之間的換算。
在常溫常壓下,\(0.500 \text{ dm}^3\) 氨中含有多少個氫原子? (常溫常壓下,氣體的摩爾體積 \(= 24 \text{ dm$^3$ mol$^{−1}$}\))
題解:
\[\begin{align} n(\ce{NH3}) & = \frac{V(\ce{NH3})}{V_m} \\ & = \frac{0.500 \text{ dm}^3}{24 \text{ dm$^3$ mol$^{-1}$}} \\ & = 0.0208 \text{ mol}\\\\ \because \text{ 一個 } & \ce{NH3} \text{ 含有 $3$ 個氫原子,}\\ \therefore \; N(\ce{H}) & = 3 \times n(\ce{NH3}) \times L \\ & = 3 \times 0.0208 \text{ mol} \times 6.02 \times 10^{23} \text { mol}^{-1}\\ & = 3.76 \times 10^{22} \end{align}\]在常溫常壓下,\(0.500 \text{ g}\) 氦的體積是多少?(常溫常壓下,氣體的摩爾體積 \(= 24 \text{ dm$^3$ mol$^{−1}$}\))
題解:
\[\begin{align} n(\ce{He}) & = \frac{m(\ce{He})}{M(\ce{He})} \\ & = \frac{0.500 \text{ g}}{2.0 \text{ g mol}^{-1}} \\ & = 0.250 \text{ mol} \\\\ \therefore \; V(\ce{He}) & = n(\ce{He}) \times {V_m} \\ & = 0.250 \text{ mol} \times 24 \text{ dm$^3$ mol$^{−1}$} \\ & = 6.00 \text{ dm}^3 \end{align}\]