此方法是通過量度反應過程中,生成一定的微量生成物所需要的時間,來獲得其反應初始反應速率的方法。在右側的影片中,展示了利用此方法來獲得硫代硫酸鈉溶液和稀氫氯酸反應的速率方程的實驗操作。
\[{\rm{N}}{{\rm{a}}_{\rm{2}}}{{\rm{S}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}\left( {{\rm{aq}}} \right)\;{\rm{ + }}\;{\rm{2HCl}}\left( {{\rm{aq}}} \right)\; \to \ {\rm{2NaCl}}\left( {{\rm{aq}}} \right)\;{\rm{ + }}\;{\rm{S}}{{\rm{O}}_{\rm{2}}}\left( {{\rm{g}}} \right)\;{\rm{ + }}\;{{\rm{H}}_{\rm{2}}}{\rm{O}}\left( {\rm{l}} \right)\;{\rm{ + }}\;{\rm{S}}\left( {\rm{s}} \right)\]通過上面的影片可以看出:在反應過程中,生成的固體硫會遮住燒杯下方的紅色十字符號。我們假設:完全遮住紅色十字符號時,所生成的固體硫的量是一定的。
在實驗過程中,我們可以量度反應物起始濃度不同時,紅色十字符號被完全遮住的時間,從而獲得反應物的起始濃度與反應初速率的關係曲線。
若要獲得硫代硫酸鈉(氫氯酸)的反應級數,實驗中就必須維持以下條件不變:
即:在測定某一物質的反應級數時,必須確保其它物質的濃度和其它反應條件保持不變。
一名同學利用此方法進行實驗,來測定硫代硫酸鈉的反應級數。實驗中,稀氫氯酸 \(\left( 1.00\ \text{mol}\ \text{d}{{\text{m}}^{-3}} \right)\) 的體積維持不變,改變水和硫代硫酸鈉溶液 \(\left( 0.05\ \text{mol}\ \text{d}{{\text{m}}^{-3}} \right)\) 的體積。實驗數據如下表所示。
| 實驗次數 | 試劑用量 \(\left( \text{c}{{\text{m}}^{\text{3}}} \right)\) | 達至不透明所需的時間 \(t\) \(\left( \text{s} \right)\) | ||
|---|---|---|---|---|
| \(\text{HCl}\left( \text{aq} \right)\) | \({{\text{H}}_{\text{2}}}\text{O}\left( \text{l} \right)\) | \(\text{N}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}\left( \text{aq} \right)\) | ||
| \(1\) | \(25.0\) | \(20.0\) | \(5.0\) | \(98\) |
| \(2\) | \(25.0\) | \(15.0\) | \(10.0\) | \(61\) |
| \(3\) | \(25.0\) | \(10.0\) | \(15.0\) | \(40\) |
| \(4\) | \(25.0\) | \(5.0\) | \(20.0\) | \(30\) |
根據上表中的數據,分別計算硫代硫酸鈉的起始濃度和時間的倒數,並繪製兩者的關係曲線,找出硫代硫酸鈉的反應級數。
| \({{\text{V}}_{\text{N}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}\left( \text{aq} \right)}}\) \(\left( \text{c}{{\text{m}}^{\text{3}}} \right)\) | \(\left[ \text{N}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}\left( \text{aq} \right) \right]\) \(\left( \text{mol}\ \text{d}{{\text{m}}^{-3}} \right)\) | 達至不透明所需的時間 \(t\) \(\left( \text{s} \right)\) | 相對速率 \(\displaystyle{ \frac{1}{t}\left( {{\text{s}}^{-1}} \right) }\) |
|---|---|---|---|
| \(5.0\) | \(0.005\) | \(98\) | \(0.010\) |
| \(10.0\) | \(0.010\) | \(61\) | \(0.016\) |
| \(15.0\) | \(0.015\) | \(40\) | \(0.025\) |
| \(20.0\) | \(0.020\) | \(30\) | \(0.033\) |
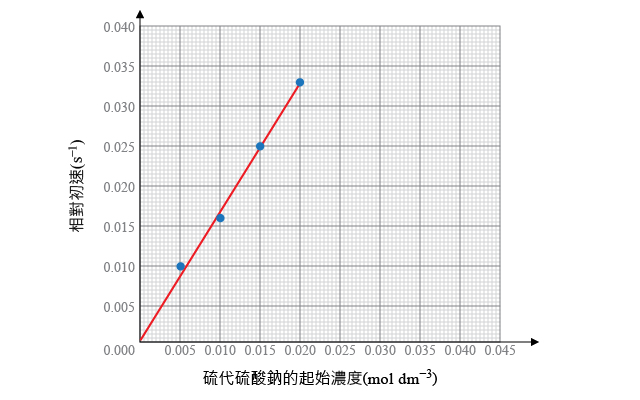
由坐標圖可知,硫代硫酸鈉的起始濃度與初速率成正比,即:
\[\text{速率}\propto \left[ \text{N}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}\left( \text{aq} \right) \right]\ \text{或者}\ \text{速率}=k\left[ \text{N}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}\left( \text{aq} \right) \right]\]
所以,反應過程中,硫代硫酸鈉的反應級數為 \(1\)。
測量原理:達至不透明所需的時間,與此時間內的平均速率成反比。
由於達至不透明狀態所需的生成物的量很少,我們假設溶液中物質的濃度維持不變,可以用相對平均速率表示相對初速率。即:
可以用時間的倒數來代替相對初速率。
\[\displaystyle{ \text{初速}∝\frac{1}{\text{達至不透明所需的時間}} }\]
另外,由於溶液的總體積是一定的,硫代硫酸的濃度與體積成正比。所以,在繪製坐標圖時,我們可以利用加入硫代硫酸鈉溶液的體積作為橫坐標來代替其具體濃度,觀察其與反應初速率的關係。