1905 年,愛因斯坦提出狹義相對論,並由此推導出物體的質量 \(m\) 與能量 \(E\) 間存在等價關係 \[E=m\,c^2\]
稱為質能關係。其中質量不再是一成不變,而是正比於物體的能量。也就是說,當外界對物體作功,給予它能量,它的質量也會隨之增加;反之,當物質對外釋放出能量,它的質量會減少。
質能關係中,質量的單位是 \(\textrm{kg}\),能量的單位是 \(\textrm{J}\),而 \(c\) 為光速 \(3\times 10^8~\textrm{m/s}\)。根據此關係,\(1~\textrm{kg}\) 質量的改變對應 \(9\times 10^{16}~\textrm{J}\) 能量的變化!

在計算原子的質量時,常會使用原子質量單位。一個原子質量單位(\(1~\textrm{u}\))定義為一個碳 12 原子質量的十二分之一。由於一摩爾碳 12 質量為 \(12~\textrm{g}\),其中包含 \(6.02\times 10^{23}\) 個碳原子,可得 \[ 1~\textrm{u} = \frac{1}{12}\left(\frac{ 12~\textrm{g} }{ 6.02\times 10^{23} }\right) = 1.66\times 10^{-27}~\textrm{kg} \]
根據質能關係,當物體的質量減少了 \(1~\textrm{u}\),它所釋放的能量為 \[1~\textrm{u} \rightarrow 1.5\times 10^{-10}~\textrm{J} = 932~\textrm{MeV}\]
其中 \(\textrm{MeV}\) 是 \(10^6\) 電子伏特,一電子伏特為一個電子經過一伏特的電勢差所獲得的能量。
| 粒子 | 質量 | 粒子 | 質量 |
|---|---|---|---|
| 中子 | \(1.008\;67~\textrm{u}\) | \(\!^{2}_1\textrm{H}\) 原子 | \(2.014\;10~\textrm{u}\) |
| 質子 | \(1.007\;28~\textrm{u}\) | \(\!^{3}_1\textrm{H}\) 原子 | \(3.016\;05~\textrm{u}\) |
| 電子 | \(0.000\;55~\textrm{u}\) | \(\!^{4}_{2}\textrm{He}\) 原子 | \(4.002\;60~\textrm{u}\) |
| \(\!^{12}_6\textrm{C}\) 原子 | \(12~\textrm{u}\) | \(\!^{141}_{56}\textrm{Ba}\) 原子 | \(143.922\;95~\textrm{u}\) |
| \(\!^{92}_{36}\textrm{Kr}\) 原子 | \(91.926\;16~\textrm{u}\) | \(\!^{235}_{92}\textrm{U}\) 原子 | \(235.043\;93~\textrm{u}\) |
原子核內,核子(質子和中子)間存在著很強的作用力,使原子核結構的改變會帶來能量的變化。譬如,對於較小的原子核,若要分開其中緊緊結合在一起的核子,原子核便需要吸收能量;而對於一些較大的原子核,其結構會因質子間的排斥力而變得不穩定,它便傾向於分裂成較小的原子核,並釋出能量。
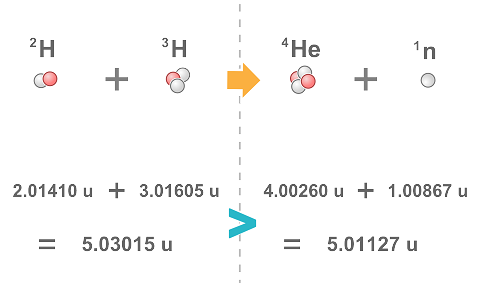
核反應中,原子核的結構會發生變化。通過質能關係,我們便能由核反應前後粒子總質量的改變,得知此反應釋放或吸收的能量。如考慮核聚變反應 \[\,^{2}_{1} \textrm{H} + \,^{3}_{1} \textrm{H} \rightarrow \,^{4}_{2} \textrm{He} + \,^{1}_{0} \textrm{n}\]
反應前粒子總質量減少了 \(0.01888~\textrm{u}\)。說明了當一個氘原子加一個氚原子,轉變為一個氦原子加一個中子時,會釋出約 \(17.6~\textrm{MeV}\) 的能量。