之前我們已分別討論過光波穿越單縫和雙縫的現象。那麼，若在上一課的干涉實驗中，改用一個含一組等闊等距的多狹縫光柵讓光穿越，結果會如何呢？

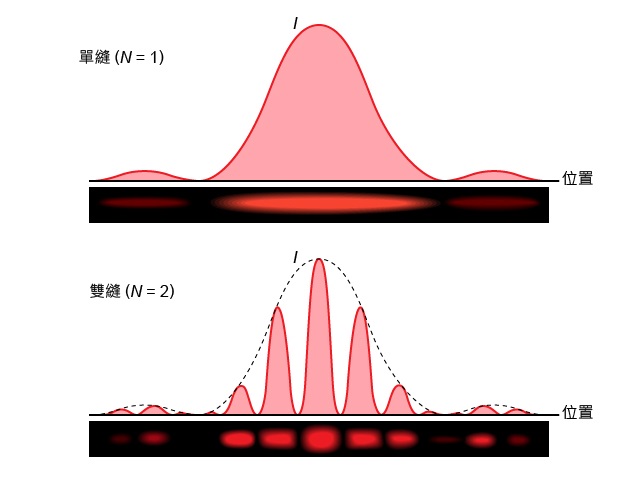
所示為使用不同狹縫數目 (\(N\)) 的光柵進行實驗、但維持同樣的狹縫闊度和縫距時，將形成的干涉條紋的光強度-位置線圖。結果顯示：

留意並未考慮光因穿越狹縫會繞射，而造成的各級數亮紋的光強度不一樣。若加上狹縫繞射的效應，中各最大值的光強度分佈會類似的 \(N=2\) 例子般被「調制」，某些干涉級數的亮紋便會變暗甚至看不見，如中的圖樣所示。總括以上有關狹縫數的效應顯示，當透過多縫光柵觀看線狀光源時，形成的圖樣也具有在雙縫中呈現的干涉和繞射性質，而且會較清晰。

【多縫繞射的實用價值】
理論上，單縫繞射已可應用作測量光源的波長和成分。由於繞射條紋的位置取決於波長，只要知道狹縫闊度和測量已知級數的條紋角位置，便能計算出光波波長。不過，單縫繞射形成的條紋很闊，而且其亮度會隨級數迅速減小，實用上難達至高的測量精確度和分辨度。然而，只要增加狹縫數目，形成的繞射條紋便會更窄更亮，這將可大幅提升測量所需的精確度和分辨度。換言之，多縫繞射具有測量光源的波長和成分的實用價值。利用多縫繞射原理作分光等應用的光學元件稱為 繞射光柵 (diffraction grating) 。

平面透射光柵 (plane transmission grating) 是一種繞射光柵，通常在一塊平坦玻璃片上刻出大量相互平行、等闊等距的刻痕，形成很細密、非常大數目的狹縫。例如在光柵的每毫米內有幾百條、以致幾千條狹縫。

如所示，考慮有一道波長為 \(\lambda \) 的平行光波垂直地射向平面透射光柵，通過光柵後便發生繞射，從每道闊度為 \(b\) 的縫向四周擴散並發生干涉；明暗相間的條紋就會在光柵另一邊的屏幕上形成。在中間的條紋是第 0 級亮紋，這是由於所有繞射光波在中間的程差是 0，這些光波發生相長干涉而形成亮紋。在其旁邊的是第 1 級亮紋、第 2 級亮紋‧‧‧‧‧‧ ，如此類推。

若要找出第 \(n\) 級亮紋的位置，方法會與雙縫的情況顃似。設光柵的狹縫間距為 \(a\)；在與光柵相距 \(D\) 的屏幕上，\(\text{P}\) 就是第 \(n\) 級亮紋的位置，與中央亮紋之間的距離為 \({{y}_{n}}\)、成角位置 \(\theta \)。當只考慮光柵與屏幕相距很遠的情況 (\(a\ll D\))，來自各狹縫並抵達 \(\text{P}\) 的光可視為平行光。對應兩相鄰亮紋的光的程差皆為 \(a\sin \theta \)，亦必定等於波長的整數倍 (\(=n\lambda \))。這表示：

    相長干涉：    \(a\sin \theta =n\lambda \)   ,    \(n\) = 0, 1, 2, 3, ‧‧‧‧‧‧

而第 \(n\) 級亮紋位置就是 \({{y}_{n}}=D\tan \theta \)。由於 \(\sin \theta \) 的最大值等於 1，由上式可寫出亮紋的最大級數滿足以下關係：

    亮紋最大級數：    \(\displaystyle{{{n}_{\max }}\le \frac{a}{\lambda }}\)                               例題

另一方面，不要忘記繞射現象會與干涉同時發生。當 \(\theta \) 方向的繞射光滿足剛才相長干涉的條件，又同時滿足以下單縫繞射的暗紋條件：

    繞射暗紋條件：    \(b\sin \theta =m\lambda \)   ,    \(m\) = 1, 2, 3, ‧‧‧‧‧‧

合併兩式得：\(n=({a}/{b})\ m\;\)，其中 \(m\) = 1, 2, 3, ‧‧‧‧‧‧。以例子的參數為例，\({a}/{b}=3\;\)，這表示 \(n\) = 3, 6, 9, ‧‧‧‧‧‧ 時便碰上光強度為零的繞射級數，所以在顯示的各組不同 \(N\) 的條紋中，皆缺少了第 3 級的干涉亮紋。

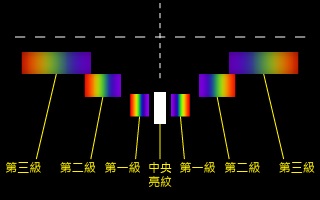
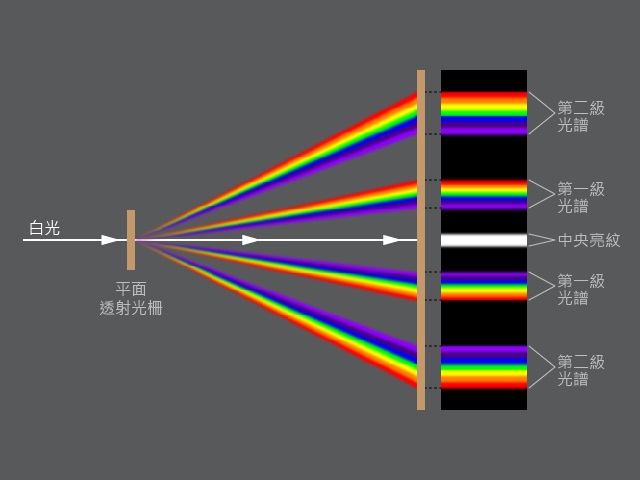
檢視公式 \(a\sin \theta =n\lambda \) 中各參數對 \(\theta \) 大小的影響，或借助的模擬程式可知，\(\lambda \) 或 \(D\) 愈大、或者 \(a\) 愈小，干涉條紋的間距愈大（即條紋分得愈開）。例如以白光為光源射向平面透射光柵的話，由於不同色光繞射角有異，除中央為白色亮紋外，其他級的亮紋會形成光譜（見），特性為：

      每個光譜為 請選擇 

• 內紅外紫
• 內紫外紅

，光譜的寬度隨級數增大 請選擇 

• 而愈闊
• 而愈窄
• 仍維持不變

。

紫光最小波長約為 \(400\ \text{nm}\)、紅光最大波長約為 \(740\ \text{nm}\)。根據 \(a\sin \theta =n\lambda \)，波長愈大 \(\theta \) 便愈大，所以光譜近中央亮紋一邊紫色、較遠離那邊紅色。我們可以寫出第 1、2 和 3 級光譜的繞射角邊界位置：

\(\sin {{\theta }_{1\min }}={{{\lambda }_{\text{violet}}}}/{a}\;=400\left( \tfrac{1}{a} \right)\ \text{nm}\)
\(\sin {{\theta }_{1\max }}={{{\lambda }_{\text{red}}}}/{a}\;=740\left( \tfrac{1}{a} \right)\ \text{nm}\)
\(\sin {{\theta }_{2\min }}={2{{\lambda }_{\text{violet}}}}/{a}\;=800\left( \tfrac{1}{a} \right)\ \text{nm}\)
\(\sin {{\theta }_{2\max }}={2{{\lambda }_{\text{red}}}}/{a}\;=1480\left( \tfrac{1}{a} \right)\ \text{nm}\)
\(\sin {{\theta }_{3\min }}={3{{\lambda }_{\text{violet}}}}/{a}\;=1200\left( \tfrac{1}{a} \right)\ \text{nm}\)
\(\sin {{\theta }_{3\max }}={3{{\lambda }_{\text{red}}}}/{a}\;=2220\left( \tfrac{1}{a} \right)\ \text{nm}\)

而 \(\sin {{\theta }_{1\max }}\) − \(\sin {{\theta }_{1\min }}\) = \(340\left( \tfrac{1}{a} \right)\ \text{nm}\)；\(\sin {{\theta }_{2\max }}\) − \(\sin {{\theta }_{2\min }}\) = \(680\left( \tfrac{1}{a} \right)\ \text{nm}\)；\(\sin {{\theta }_{3\max }}\) − \(\sin {{\theta }_{3\min }}\) = \(1020\left( \tfrac{1}{a} \right)\ \text{nm}\)。這顯示光譜隨 \(n\) 增大而變寬。但要留意 \(\sin {{\theta }_{2\max }}\) > \(\sin {{\theta }_{3\min }}\)，即是第 2 級光譜與第 3 級光譜是重疊的：