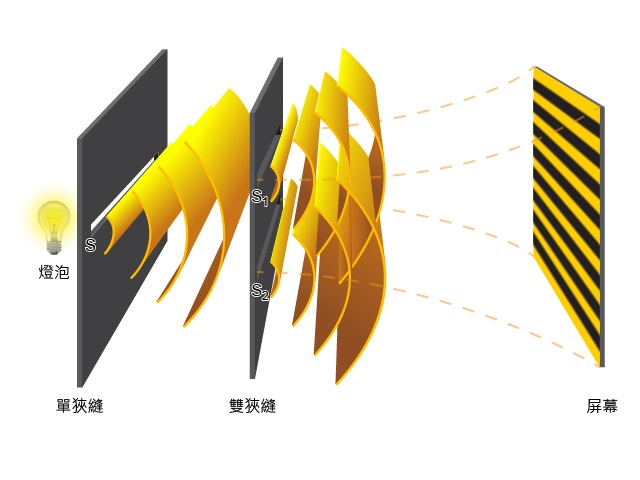
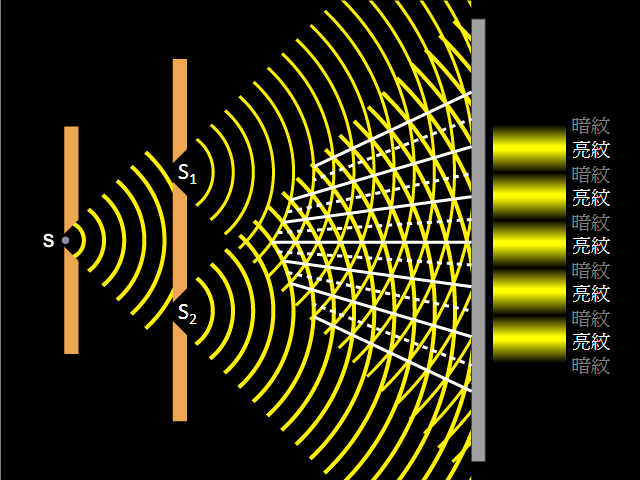
在楊氏雙縫實驗中，干涉圖樣是等距、明暗交替的條紋。那麼，如何定量描述條紋的位置呢？兩條相鄰亮紋或相鄰暗紋之間的距離是多少呢？

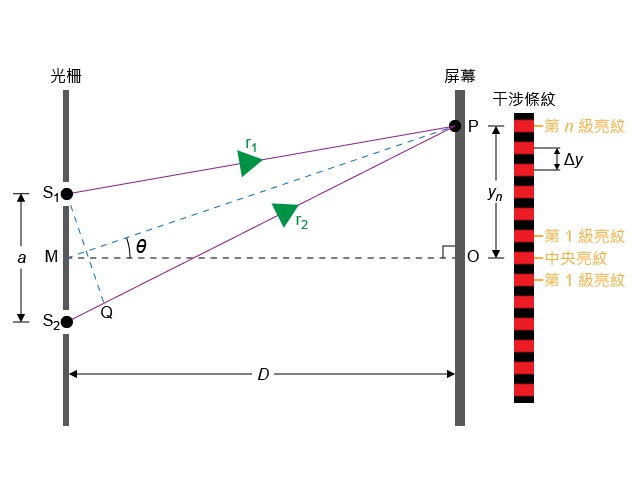
我們可以分析形成某亮紋的光的路徑，推導描述亮紋位置的關係式。在，設雙縫 \({{\text{S}}_{1}}\) 和 \({{\text{S}}_{2}}\) 的間距為 \(a\)，\(\text{M}\) 是雙縫的中點；在與雙縫光柵相距 \(D\) 的屏幕上，\(\text{O}\) 和 \(\text{P}\) 分別就是中央亮紋和某任意級數（稱其為第 \(n\) 級）亮紋的位置。它們之間的距離 (\({{y}_{n}}\)) 可用作描述第 \(n\) 級亮紋的位置。

先考慮光線 \({{r}_{1}}\) 與 \({{r}_{2}}\) 的程差。在的 \({{r}_{2}}\) 上設 \(\text{Q}\)，令 \(\text{QP}\) 與 \({{\text{S}}_{\text{1}}}\text{P}\) 等長，所以 \({{\text{S}}_{\text{2}}}\text{Q}\) 是 \({{r}_{1}}\) 與 \({{r}_{2}}\) 的程差。由於實驗中一般 \(a\ll D\)，可重繪成如所示，由此得 \(a\sin \theta \) = \({{\text{S}}_{\text{2}}}\text{Q}\)。另一方面，由於 \(\text{P}\) 是第 \(n\) 級亮紋的位置，根據相長干涉條件，程差必定等於波長的整數倍 (\(=n\lambda \))。這表示：

    相長干涉：    \(a\sin \theta =n\lambda \)   ,    \(n\) = 0, 1, 2, 3, ‧‧‧‧‧‧

現考慮 \(\text{P}\) 與中央亮紋之間的距離 \({{y}_{n}}\)。從上可知 \(\tan \theta ={{{y}_{n}}}/{D}\;\)。只要干涉級數 (\(n\)) 並非很大，\(\theta \) 的值會很小，我們可以假設 \(\tan \theta \approx \sin \theta \)，由此可寫出 \(\sin \theta \approx {{{y}_{n}}}/{D}\;\)；把它代入上式後再移項，得：

    亮紋位置：    \(\displaystyle{{{y}_{n}}=n\frac{\lambda D}{a}}\)

上式顯示 \(\lambda \) 或 \(D\) 愈大、或者 \(a\) 愈小，干涉條紋分得愈開。接下來我們要找出兩條相鄰亮紋之間的距離。根據上式，可寫出第 \((n+1)\) 級亮紋與中央亮紋之間的距離為 \({{y}_{n+1}}\) = \(\left( n+1 \right){\lambda D}/{a}\;\)，換言之：

這結果顯示條紋間距與干涉級數 (\(n\)) 無關，故屏幕上的干涉條紋寬度皆相同。

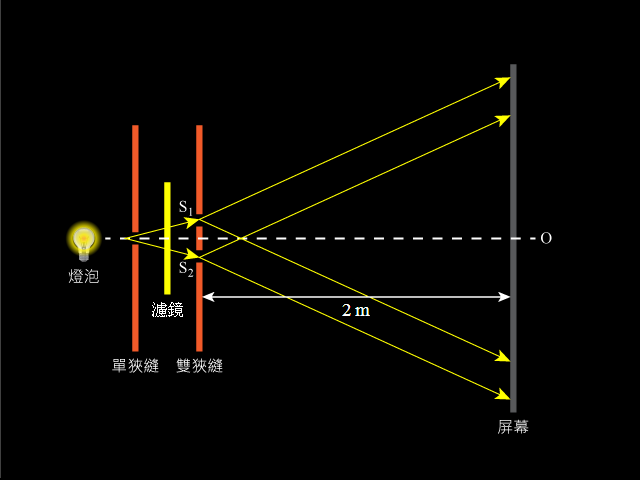
所示為一個楊氏雙狹縫實驗。一束光通過濾鏡後成為單色光，設單色光垂直地射向雙縫 \({{\text{S}}_{1}}\) 和 \({{\text{S}}_{2}}\)；雙縫的間距是 \(0.246\ \text{mm}\)。干涉圖樣在 \(2\ \text{m}\) 外的屏幕上形成，而相鄰暗紋間的距離是 \(4.5\ \text{mm}\)。請計算單色光的波長。

【題解】

在楊氏雙狹縫實驗中，兩相鄰亮紋（或暗紋）之間的距離 \(\Delta y\) 可由以下關係式描述：

\(\displaystyle{\Delta y=\frac{\lambda D}{a}}\)

其中 \(\lambda \) 是光的波長、\(a\) 是雙狹縫間距離、\(D\) 是雙縫與屏幕間距離。我們已知 \(a=0.246\ \text{mm}\)、\(D=2\ \text{m}\) 和 \(\Delta y=4.5\ \text{mm}\)，要計算 \(\lambda \)。只需把前述數字代入上式，即：

\(\displaystyle{4.5\times {{10}^{-3}}\ \text{m}=\frac{\lambda \left( 2\ \text{m} \right)}{0.246\times {{10}^{-3}}\ \text{m}}}\)

上方把數字代入時，留意單位已統一使用 \(\text{m}\)。運算後便求得：

\(\lambda =5.54\times {{10}^{-7}}\ \text{m}\)

換言之，該單色光的波長等於 \(554\ \text{nm}\)。根據可見光譜：