之前曾討論的波動現象,皆只涉及一個脈衝或一列連續波的傳播,然而在實際生活中發生的波動現象中,往往是由兩個或更多的波同時交會或重疊而成的(、),造成波形的改變。
最簡單的例子就是,在同一介質裡,如果有兩列波(或兩個脈衝,見)向對方迎面傳播,當兩波相遇時,它們便會開始重疊。可以預期,在發生重疊的範圍內,質點的運動會同時取決於來自兩方的波動。那麼,質點會如何振動呢?從實驗中可觀察到,原來質點在重疊範圍內的振動,可以由波的疊加原理 (principle of superposition) 描述:
幾列波在同一介質內傳播而相遇時:
疊加後的質點位移 \(=\) 各波單獨存在時在該點形成位移的矢量和
各波各自維持原來的性質(波長、頻率、振動方向等)不變,繼續其原來的傳播方向繼續傳播
故此在,錦鯉激起的脈衝與圓形水波彼此穿過又再分開後,仍能維持以其原本波源為中心的圓形波各自繼續獨立傳播。

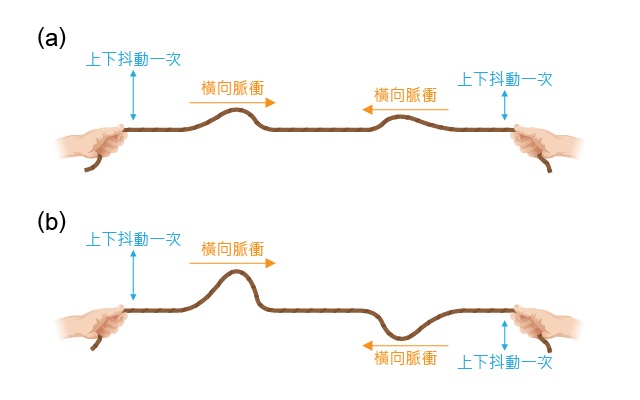
我們不妨觀察相遇脈衝疊加時,合脈衝的波形。顯示了兩脈衝相遇中的某時刻。根據疊加原理,由於合位移的計算乃矢量相加,可知若兩脈衝的:
兩波重疊時將組成新的合成波,便顯示了兩迎面脈衝波形皆向上時,以及兩脈衝波形上下相反時的疊加過程。留意兩脈衝在交會重疊期間,質點因疊加現象而造成合位移;合位移隨着兩脈衝的交會而變化,過程中遵循疊加原理。而在相遇之後,兩脈衝便維持其原本波形和傳播速度各自繼續前進,並不會因為曾經相互疊加而發生變化。
至於連續波,當兩波在同一介質中相遇時,在相遇區域內同樣會形成一列合成波;各質點的合位移亦同樣遵循疊加原理。對於頻率與振動方向皆相同、且有固定相位差的兩列相同波形的波疊加時,會造成干涉 (interference),情況便如。留意合成波的振幅可能會大於或小於原有兩波的振幅的,分別稱為相長 (constructive) 和相消干涉 (destructive interference)。在這情況:
【相長干涉】當相遇的兩波同相,合成波的振幅會大於原有兩波的振幅;
【相消干涉】當相遇的兩波反相,合成波的振幅會小於原有兩波的振幅。