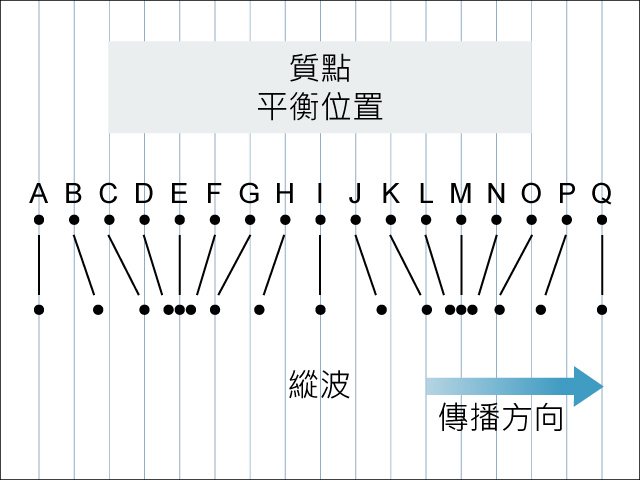
由於縱波是一種傳遞疏密度的波，這令縱波質點的運動不易掌握（見）。要解決這困難，我們可以藉橫波的方式來表現縱波，循此方向製作縱波的位移-距離 (\(s\)-\(d\)) 關係線圖，以便分析縱波質點的運動。現考慮運動中的一列縱波，顯示了某時刻質點及其平衡位置，以下是建立縱波 \(s\)-\(d\) 線圖的步驟：

有了縱波的 \(s\)-\(d\) 關係線圖，便能以分析橫波的方法，找出縱波中質點的運動狀態。但要強調一點，\(s\)-\(d\) 關係線圖只顯示了波上某一刻各質點之位移。當縱波波形隨時間變化時，其 \(s\)-\(d\) 圖也跟著改變，如所示。

如上一節所述，\(s\)-\(d\) 關係線圖顯示的，乃某一刻於波上各位置的質點之位移。若要關注某質點的位移隨時間的變化，可以繪出該質點的位移-時間 (\(s\)-\(t\)) 關係線圖。跟橫波一樣，縱波的 \(s\)-\(t\) 關係線圖能描述波中 其中一個質點 的位移隨時間的變化，以助了解質點的振動情況。

便以某列向右傳播的縱波的其中一個質點 "R" 為例，顯示了該質點的 \(s\)-\(t\) 關係線圖。該關係線圖的設置亦與橫波的相同：

【\(s\)-\(t\) 線圖的橫軸】
橫軸為時間 \(t\)；

【\(s\)-\(t\) 線圖的縱軸】
縱軸為質點相對於其平衡位置的位移 \(s\)。

這裡要再次強調一點，波上不同位置的質點在同一波長內，它們的 \(s\)-\(t\) 關係線圖是不同的。便顯示了某向右傳播縱波上，多顆不同位置質點的 \(s\)-\(t\) 關係線圖了。由線圖可知：