線性放大率是物體的高度和像的高度的比,通常用 \(m\) 表示:
\(\displaystyle{m=\frac{{{h}_{i}}}{{{h}_{o}}}}\)
\({{h}_{i}}\):像的高; \({{h}_{o}}\):物體的高。
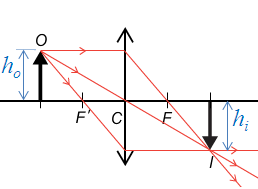
線性放大率是一個比,所以沒有單位,它表示了像較實物放大或縮小了多少。那麼 \(m\) 的數值如何反映像的大小呢?至便以凸透鏡為例,分別說明 \(m\) < 1、\(m\) = 1 和 \(m\) > 1,這三種情況的意義。除了從物體和像的高度來計算 \(m\) 外,還有其他方法能找出線性放大率嗎?事實上,線性放大率也可寫成:
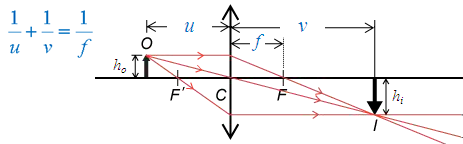
\(\displaystyle{m=\frac{\left| v \right|}{u}}\)
\(v\):像距; \(u\):物距。
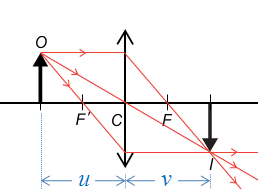
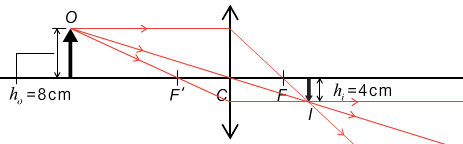
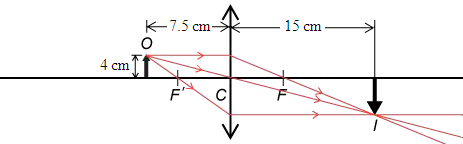
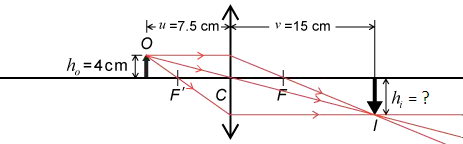
若有一件 4 \(\text{cm}\) 高的物體放在凸透鏡前 7.5 \(\text{cm}\),如所示,其像出現於凸透鏡後 15 \(\text{cm}\) 處。那麼,像的高度是多少?
【題解】
已知():
物距 \(u\) = 7.5 \(\text{cm}\); 像距 \(v\) = 15 \(\text{cm}\)。
要找出像的高度,首先從物距和像距計算線性放大率:
\(\displaystyle{m=\frac{v}{u}=\frac{15\ \text{cm}}{7.5\ \text{cm}}=2}\)
利用線性放大率的定義,把物高 \({{h}_{o}}\) = 4 \(\text{cm}\) 及 \(m\) = 2 代入有關算式,便能求出像高 \({{h}_{i}}\)。換言之:
\(\displaystyle{m=\frac{{{h}_{i}}}{{{h}_{o}}}}\) \(\Rightarrow \) \(\displaystyle{2=\frac{{{h}_{i}}}{4\ \text{cm}}}\)
\({{h}_{i}}\) = 8 \(\text{cm}\)
因此,像的高等於 8 \(\text{cm}\)。
【分析計算結果】
由於 \(u\) = 7.5 \(\text{cm}\)、\(v\) = 15 \(\text{cm}\)、得 \(f\) = 5 \(\text{cm}\),即 \(f\) < \(u\) < \(2f\) 以及 \(v\) > \(2f\),表示物體在 \(\text{2F’}\) 和 \(\text{F’}\) 之間、放大的像位於 \(\text{2F}\) 以外。這結果與運用作圖法找出的成像特性吻合。