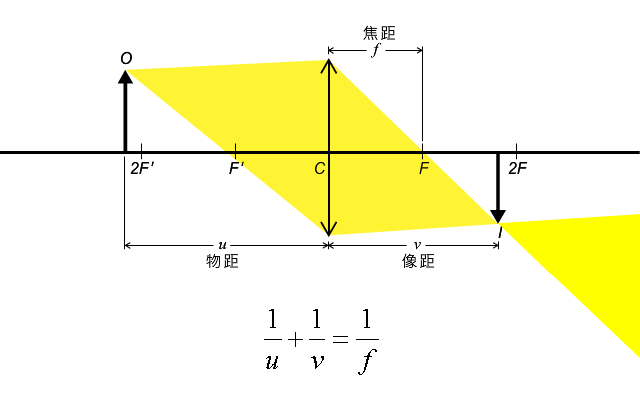
除了繪畫透鏡光線圖外,我們還可以利用數學方程式來計算出像的位置。那麼,有關的方程式是怎麼樣呢?如所示,設有一物體 \(O\) 在焦距為 \(f\) 的透鏡前,形成像 \(I\);以 \(u\) 代表物體與透鏡間的距離(簡稱物距)、\(v\) 代表像與透鏡間的距離(簡稱像距),它們之間的關係可用透鏡公式表示:
\(\displaystyle{\frac{1}{u}+\frac{1}{v}=\frac{1}{f}}\)
上式是一道有三個變數的方程,因此,只要知道 \(u\)、\(v\)、\(f\) 中其中兩個變數的數值,把數值代入公式中建立方程,解方程後就能找出餘下的未知數了。若要證明透鏡公式的話,我們亦不難從光線圖上找出有關的關係:
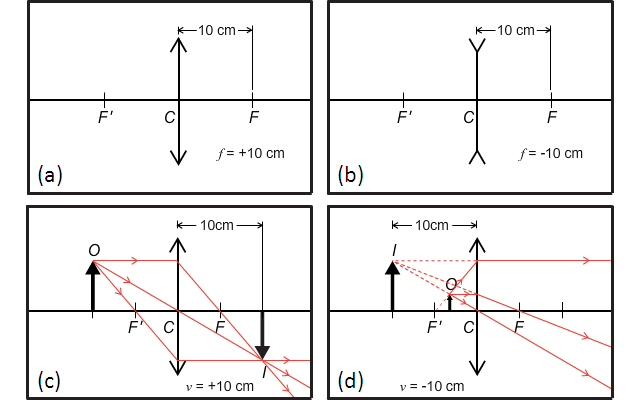
透鏡公式乃同時適用於凸透鏡和凹透鏡的。但在應用透鏡公式時,需要確定透鏡類型、並按此選取式中物理量的正負值。我們會採用實正虛負法則 (real-is-positive convention)。根據這法則,如果是():
凸透鏡:\(f\) 取正 (+) 值; 凹透鏡:\(f\) 取負 (-) 值。
還有 \(u\) 必然取正值。但計算出來的像距 \(v\),有時是正、有時是負。若得出 \(v\) > 0,表示透鏡造成的是實像;若得出 \(v\) < 0,表示透鏡造成的是虛像。當情況為已知像的位置和虛實,如果像是:
實像:\(v\) 取正 (+) 值; 虛像:\(v\) 取負 (-) 值。
便總結了應用透鏡公式時的實正虛負法則。
| \(\displaystyle{\frac{1}{u}+\frac{1}{v}=\frac{1}{f}}\) | 正負值 | 法則內容 | ||
|---|---|---|---|---|
| 凸透鏡 | 凹透鏡 | |||
| 焦距 \(f\) | \(+\) | \(-\) | 凸透鏡 \(f\) 取正值、凹透鏡 \(f\) 取負值 | |
| 物距 \(u\) | \(+\) | \(+\) | \(u\) 始終取正值 | |
| 像距 \(v\) | 實像 | \(+\) | 不存在 | 實像的 \(v\) 取正值、虛像的 \(v\) 取負值。留意凸透鏡才可能形成實像或虛像,而凹透鏡只形成虛像。 |
| 虛像 | \(-\) | \(-\) | ||
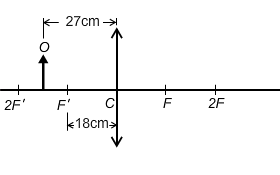
如所示,某物體 \(O\) 置於凸透鏡前 27 \(\text{cm}\) 處,凸透鏡的焦距是 18 \(\text{cm}\)。像的位置在那處?
【題解】
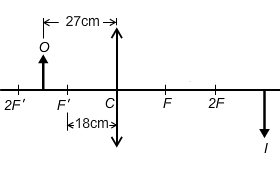
若熟識凸透鏡成像性質,可先估計像的位置、在圖上草繪出像 (\(I\)) 的位置和大小(見),幫助解題。現在正式解題,先確定未知數是甚麼:
已知:
透鏡的焦距 \(f\) = 18 \(\text{cm}\)
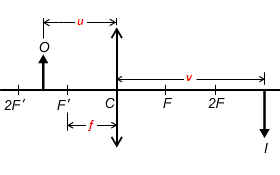
便在圖上標示了各項已知和未知的符號。把 \(u\)、\(f\) 的數值代入透鏡公式:
\(\displaystyle{\frac{1}{u}+\frac{1}{v}=\frac{1}{f}}\)
\(\displaystyle{\frac{1}{27}+\frac{1}{v}=\frac{1}{18}}\)
\(v=54\)
因此,像距離透鏡 54 \(\text{cm}\)。
【分析計算結果】
完成計算後,謹記檢查計算結果是否合理。在這題中,物體位置在 \(\text{F’}\) 和 \(\text{2F’}\) 之間,像的位置應在 \(\text{2F}\) 以外(見),計算結果符合預期。