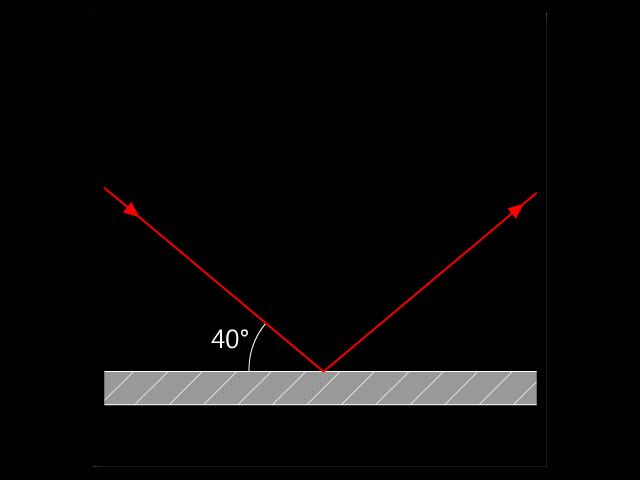
表示一束光線射到平面鏡上的情況。入射線與鏡面成 40 度角。入射角是多少？反射角是多少？

【題解】

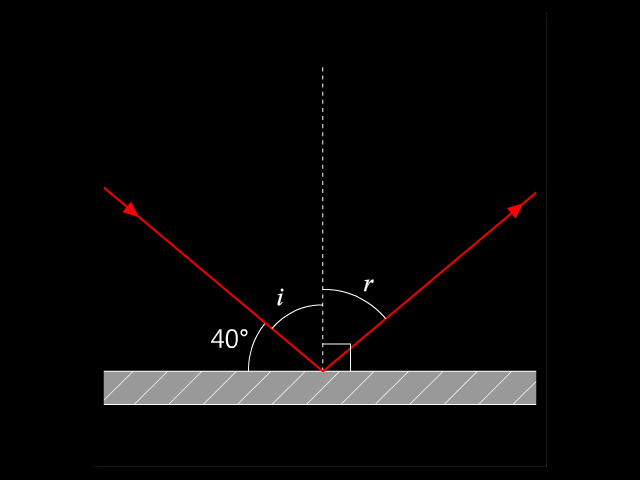
解決這類問題時，可以先如般在光線圖上繪出法線，目的是要找出入射角和反射角的位置。入射角 \(i\) 就是入射線與法線間的夾角，而反射角 \(r\) 就是反射線與法線間的夾角。因為法線是垂直於鏡面，所以：

\(i\) + \(40{}^\circ \) = \(90{}^\circ \)

因此入射角 \(i\) 等於 \(90{}^\circ \) − \(40{}^\circ \) = \(50{}^\circ \)。

接下來，根據反射定律，反射角 \(r\) 等於入射角 \(i\)，因此：

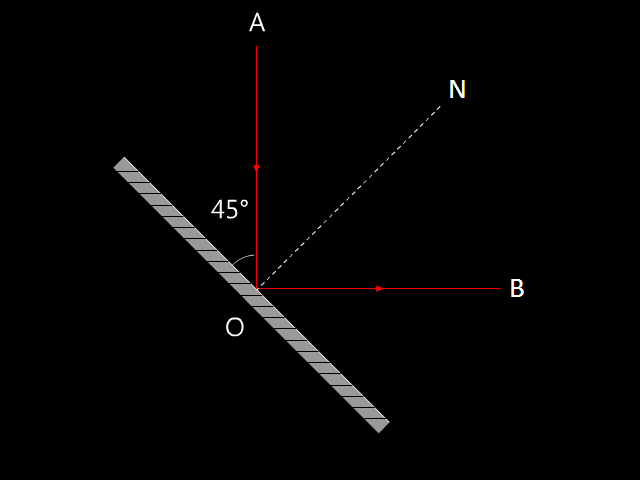
有一束光線豎直地向下射到一塊平面鏡上，平面鏡與光線成 45 度角，反射線以水平方向射出。如果入射線的方向傾斜了 30 度，如藍色入射線所示，平面鏡要轉多少度（以入射點為軸心），才能使反射線的方向保持不變？

【題解】

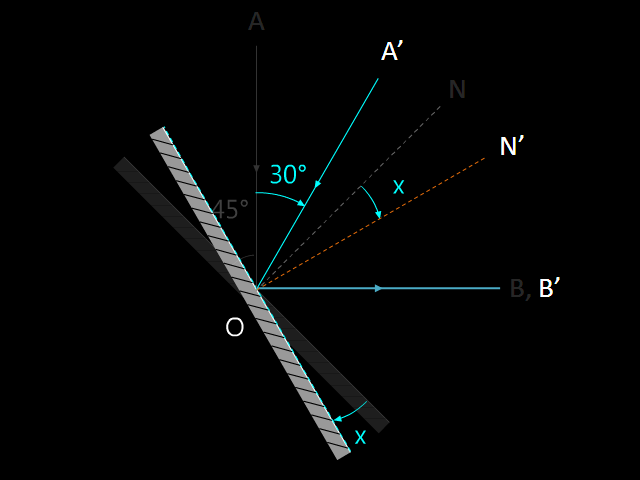
如中示範，入射線的方向傾斜後，將平面鏡以順時針方向轉動若干角度，反射線便能恢復至原來的方向。在，\(\text{AOB}\) 是入射線傾斜前的光線路徑；在，\(\text{A'OB'}\) 是入射線傾斜並轉動鏡後的光線路徑。設 \(\text{NO}\) 為平面鏡原本的法線，若平面鏡轉了角 \(x\)，使到反射線維持原本的方向，法線也會跟平面鏡一起轉動角 \(x\)，從 \(\text{NO}\) 轉到 \(\text{N'O}\) 的位置。事實上，角 \(x\) 就是反射角於鏡轉動前與鏡轉動後，這兩情況的差，即 \(x\) = \(\angle \text{NOB}-\angle \text{N'OB'}\)。換言之，要找出鏡需轉多少度，便需先分別計算鏡轉動前的反射角 (\(\angle \text{NOB}\)) 和鏡轉動後的反射角 (\(\angle \text{N'OB'}\))。

參看，原本入射線 \(\text{AO}\) 是豎直的，反射線 \(\text{OB}\) 是水平的，這表示：

\(\angle \text{AOB}=90{}^\circ \)

根據反射定律：

\(\angle \text{NOB}=\tfrac{\angle \text{AOB}}{2}=\tfrac{90{}^\circ }{2}=45{}^\circ \)

參看，當入射線 \(\text{AO}\) 沿入射點轉了 \(30{}^\circ \) 後到達 \(\text{A'O}\) 的位置，入射線轉了的角度就是 \(\angle \text{AOA'}\) = \(30{}^\circ \)。藉其可算出鏡轉動後、入射線和反射線之間的夾角 \(\angle \text{A'OB'}\)：

\(\angle \text{A'OB'}=\angle \text{AOB}-\angle \text{AOA'}=90{}^\circ -30{}^\circ =60{}^\circ \)

根據反射定律：

\(\angle \text{N'OB'}=\tfrac{\angle \text{A'OB'}}{2}=\tfrac{60{}^\circ }{2}=30{}^\circ \)

\(x=\angle \text{NOB}-\angle \text{N'OB'}=45{}^\circ -30{}^\circ =15{}^\circ \)

因為角 \(x\) 就是平面鏡需要轉動的角度，結論就是平面鏡要轉動 \(15{}^\circ \)，才能使反射線的方向保持不變。