閱畢上一節後,你或留意到功率不僅應用於動力裝置上,亦能見於其他範疇的裝置(如電器裝置;我們亦會在其他有關範疇的模組裡討論功率)。當功率的討論乃集中於力學時,有時會便於以力和速度來表示功率。
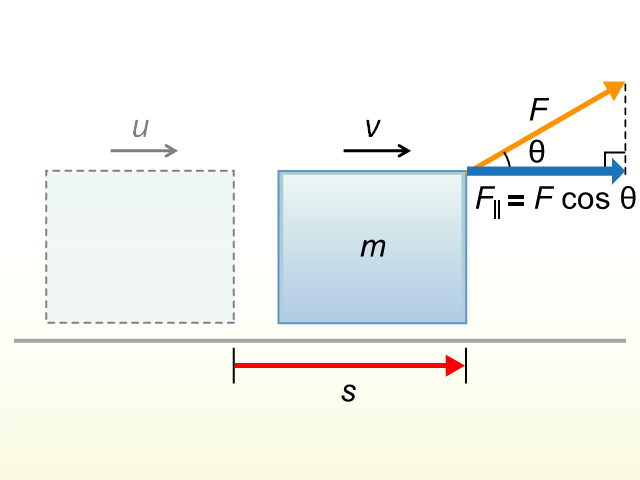
考慮一個恆力 \(F\) 作用於某物體時,令物體造成了位移 \(s\)()。如果 \(F\) 於物體運動方向上的分量為 \({{F}_{||}}\),這個力所作的功就是 \(W\) = \({{F}_{||}}\) \(s\)。設物體於時段 \(t\) 期間造成該位移 \(s\),即功率為:
\(\displaystyle{P=\frac{W}{t}=\frac{{{F}_{||}}\ s}{t}}\)
由於 \(s\) / \(t\) 就是物體的速度 \(v\)。換言之,功率可寫成:
\(P={{F}_{||}}\ v\)
留意上式只適用於 \({{F}_{||}}\) 與 \(v\) 方向相同的情況。另一方面,儘管上方乃基於的例子而導出算式,然而,這算式實具有多重闡釋:
若物體正進行勻速運動,表示物體受到的淨力等於零。換言之,必定有一道與 \({{F}_{||}}\) 大小相同、方向相反的力作用於物體。例如來自滑動時地面給予物體的摩擦力。
在本模組例子,我們會先關注物體以勻速運動時所作的功率(見)。
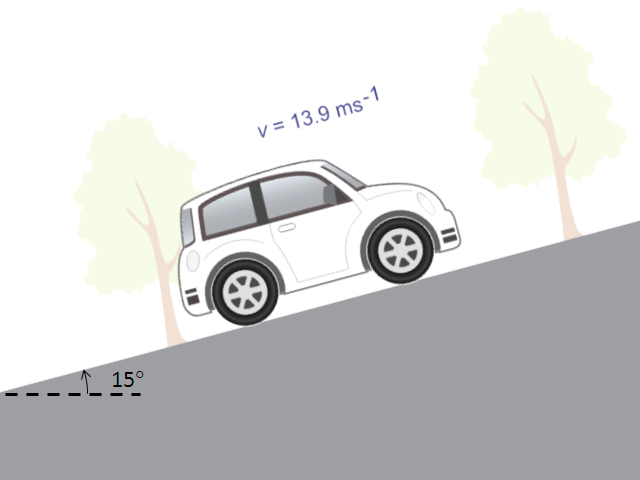
一輛質量為 1500 \(\text{kg}\) 的汽車以 13.9 \(\text{m }{{\text{s}}^{-1}}\) 的勻速率沿斜坡向上行駛。已知斜坡的斜度等於 \(15{}^\circ \)(),忽略作用於該車上的空氣阻力及來自地面的摩擦力,試計算引擎於行駛期間的最大馬力輸出。
【題解】
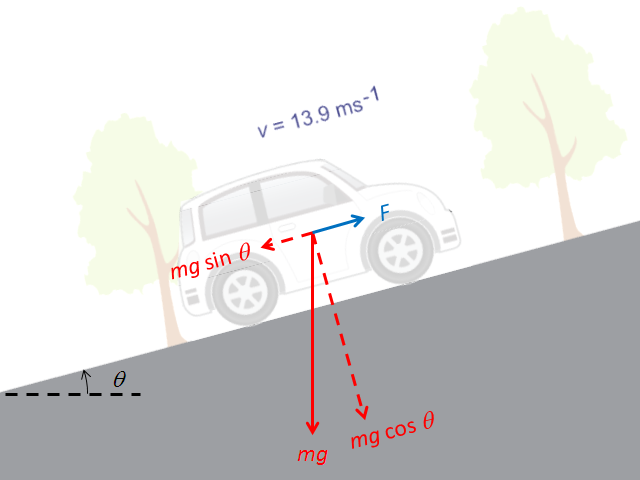
設汽車的質量為 \(m\)、斜坡的斜度為 \(\theta \)。於相反於汽車運動的方向,汽車的重量 \(mg\) 會沿斜面造成分力 \(mg\) sin \(\theta \),如所示。由於汽車以勻速行駛,作用於汽車上的淨力等於零,可知這個分力的大小,必定與汽車引擎的推進力 (\(F\)) 相同。換言之:
\(F=mg\sin \theta \)
再者,由於汽車以固定的速度 \(v\) 行駛、\(F\) 固定不變,表示引擎的功率亦於過程中維持不變。設引擎的功率為 \(P\),應用功率與速度的算式、再運用上式,即:
\(P=F\ v=mg\ v\sin \theta \)
代入 \(m\) = 1500 \(\text{kg}\)、\(g\) = 9.8 \(\text{m }{{\text{s}}^{-2}}\)、\(v\) = 13.9 \(\text{m }{{\text{s}}^{-1}}\)、\(\theta \) = \(15{}^\circ \),便算得 \(P\) = 52885 \(\text{W}\)。由於 1 馬力等於 746 \(\text{W}\),這個結果以「馬力」表示時,就是: