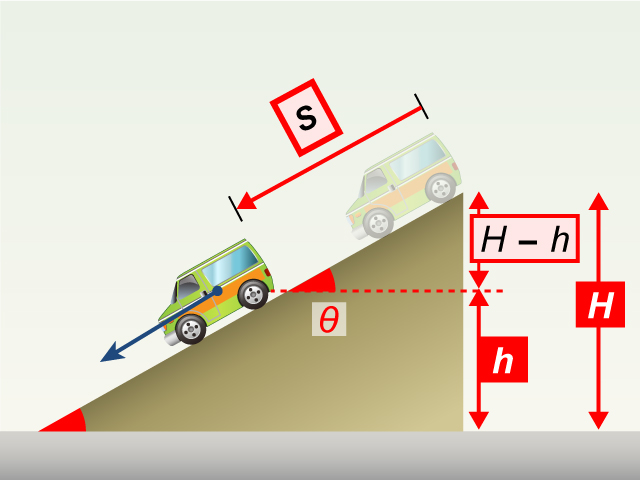
如所示，質量為 \(m\) 的紅色方塊原本被按在光滑斜面上、與地面垂直距離為 \(h\) 的位置。現方塊被釋放、沿斜面上滑動至地面的所行距離等於 \(l\)。質量同樣為 \(m\) 的藍色方塊則在高度為 \(h\) 的地面上方被釋放。忽略空氣阻力，試分別找出對紅色方塊和藍色方塊所作的淨功。（設重力加速度為 \(g\)）

 

【題解】

先討論藍色方塊。作用於方塊上的力只有藍色方塊的重量 (\(mg\))，其方向沿方塊運動的方向，換言之，對方塊的作功等於 \(mg\) (cos \(0{}^\circ \)) \(h\)，即是：

\({{W}_{blue}}\) = \(mgh\)

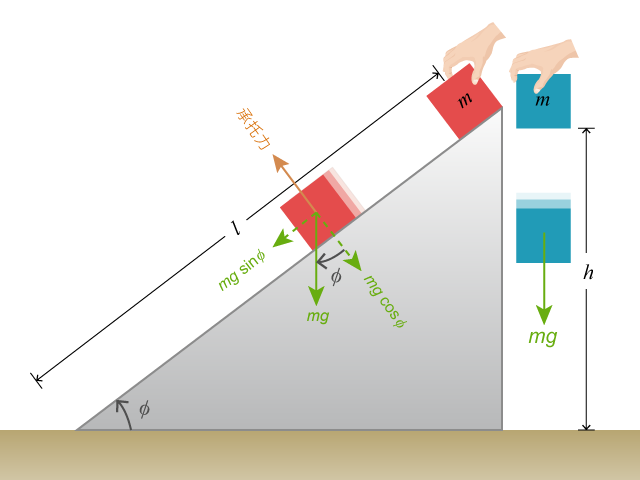
現討論紅色方塊。方塊重量的方向既非平行於斜面、亦非垂直於斜面。若設斜面跟水平成角 \(\phi \)，考慮對重量這個力分解為垂直和平行於斜面的兩個分量，分別為 \(mg\) cos \(\phi \) 和 \(mg\) sin \(\phi \)。在垂直於斜面的方向，斜面會給予方塊一個大小為 \(mg\) cos \(\phi \) 的承托力。因此，作用於方塊的淨力只有重量沿斜面的分量。換言之，對方塊的作功：

\({{W}_{red}}\) = \(mg\) (sin \(\phi \)) \(l\)

然而，\(l\) sin \(\phi \) 本質上就是 \(h\)（見），所以：

\({{W}_{red}}\) = \(mgh\)

留意 \({{W}_{blue}}\) = \({{W}_{red}}\)，原來儘管兩方塊的路徑不同，只要它們沿垂直方向有同等的位移變化，重力對它們所作的功是相同的！再者，\(-mgh\) 就是方塊下墜前後的勢能變化（見上一節），即兩方塊下墜前後的勢能變化相同。這結果引證：物體的重力勢能變化只取決於起點和終點間的高度、不會跟運動路徑有關。

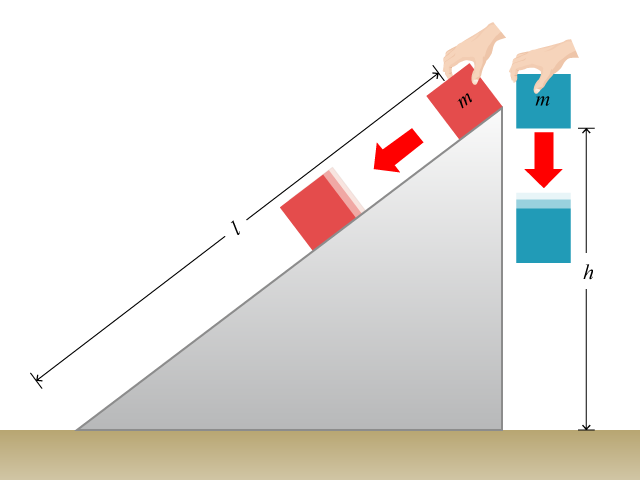
如所示，一輛質量 \(m\) 的小車從離地面高度 \(H\) 釋放，並沿着無摩擦力、斜度為 \(\theta \) 的斜面滑下。設 \(s\) 與 \(h\) 分別為過程中小車的位移和離地面的瞬時高度，試找出：(i) \(h\) 隨 \(s\) 變化的關係式；(ii) 小車重力勢能 (\(PE\)) 隨其位移的變化；(iii) \(PE\) 隨時間的變化；(iv) \(PE\) 隨小車動能的變化。（設地面 \(PE=0\)）

 

【題解】

參考可找出 \(h\) 隨 \(s\) 的變化。由三角關係可寫出 \({\left( H-h \right)}/{s}\;\) = \(\sin \theta \)，即：

\(h=H-s\ \sin \theta \)

由於已設地面的重力勢能為零，合併上式和重力勢能的表達式 \(PE=mgh\) 以消去 \(h\)，得 \(PE\) = \(mg\)\(\left( H-s\ \sin \theta \right)\)，即：

\(PE=\left( -mg\ \sin \theta \right)s+mgH\)

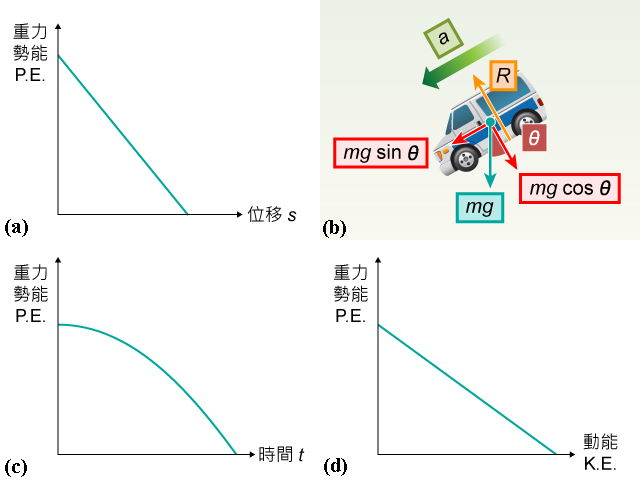
(a) 顯示上式的關係線圖。下一步我們要找出 \(PE\) 隨時間 (\(t\)) 的變化，方法之一是利用勻加速運動方程 \(s\) = \(ut\) + \(\tfrac{1}{2}a{{t}^{2}}\)，把剛才 \(PE\)-\(s\) 關係式中的 \(s\) 變換為 \(t\)。已知小車起初靜止，故 \(u=0\)。然而小車的加速度 \(a\) 為未知，我們或可先從小車的隔離體圖（(b)）分析。根據牛頓第二定律：\(mg\sin \theta \) = \(ma\)，即 \(a=g\sin \theta \)。換言之，\(PE\) = \(\left( -mg\sin \theta \right)\)\(\left( \tfrac{1}{2}g\sin \theta \ {{t}^{2}} \right)\) + \(mgH\)，得：

\(PE=-\tfrac{1}{2}m{{\left( g\sin \theta \right)}^{2}}{{t}^{2}}+mgH\)

(c) 顯示上式的關係線圖。最後一步要找出 \(PE\) 隨 \(KE\) 的變化。我們可以利用另一條勻加速運動方程 \({{v}^{2}}\) − \({{u}^{2}}\) = \(2as\)，先把 \(PE\)-\(s\) 關係式中的 \(s\) 變換為 \(v\)。記得 \(u=0\) 以及 \(a=g\sin \theta \)，即 \(PE\) = \(\left( -mg\sin \theta \right)\)\(\tfrac{{{v}^{2}}}{2g\sin \theta }\) + \(mgH\)，或：

\(PE=-\tfrac{1}{2}m{{v}^{2}}+mgH\)

由於 \(\tfrac{1}{2}m{{v}^{2}}\) 就是 \(KE\)，故 \(PE=-KE+mgH\)，(d) 顯示這關係線圖。