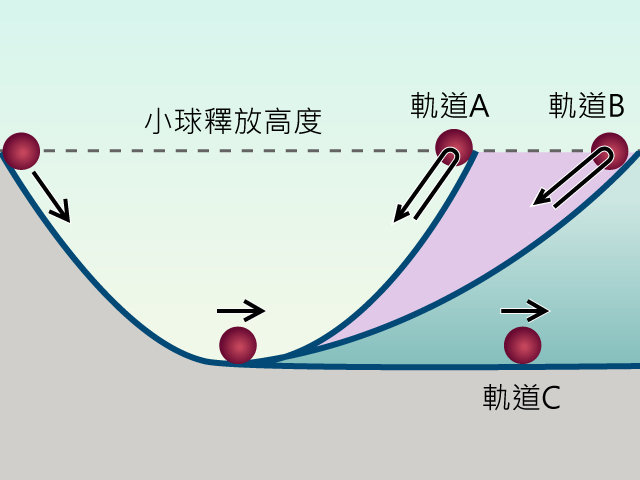
我們可先研習著名的伽俐略理想實驗，進一步掌握能量的概念。實驗操作如下：讓小球在如的左邊斜面滑下，它會滑至最低點後再繼續滑上右邊的斜面，停留一瞬間後折返。如果沒有摩擦力，無論右邊斜面是較左邊的陡些、緩些、還是同等傾斜（如不同軌道），小球在右邊斜面瞬時靜止的位置、其所抵達的垂直高度，總會跟起初在左邊釋放時的高度相同！這看來似乎是小球「記得」其釋放高度的現象，仿佛告訴我們「有某一物理量是守恆的」，我們給它稱為能量。事實上，當我們把小球從桌面提高到所示的釋放高度時，便賦予小球一種形式的能量，我們稱這種能量為勢能 (potential energy)：

情況裡的相互作用，就是小球受到重力的作用。

之前我們提過，能量就是具作功的能力，而勢能亦然，這種能量有作功的潛力。在，當小球被釋放後，小球開始運動、重力對小球作功；小球有了速度即獲得了動能，這乃轉化自小球位於地面上方的某一高度而具有的勢能。隨着小球滑下、其速度愈來愈快，動能增加、勢能減少。及至小球滑上右邊斜面，小球便因高度提升而從動能回收勢能、運動速度逐漸變慢。同理，如果在軌道 C 這系統的斜面釋放小球，進入水平段後小球的速度會維持不變，也就是有不變的動能，這個動能源自哪裡呢？也就是轉化自小球原本位於斜面高處時的勢能了！

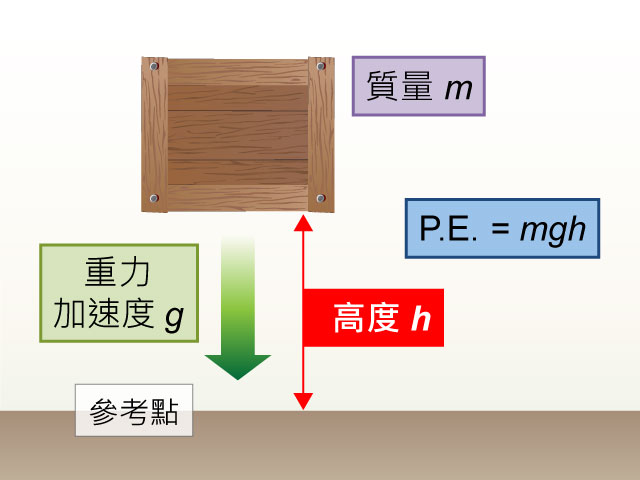
上方一直討論的這種勢能，就是重力勢能 (gravitational potential energy)：

重力勢能常以符號 \(PE\) 或 \(U\) 表示，它的國際單位制單位是焦耳 (\(\rm{J}\))，跟其他能量一樣。質量為 \(m\) 的物體位處於與參考點的垂直距離為 \(h\) 時，重力勢能等於：

\(g\) 就是重力加速度（）。由於 \(h\) 是相對於某一水平面而言的，所以有所謂的參考點（或稱參考平面），慣常我們會取地面為參考點。

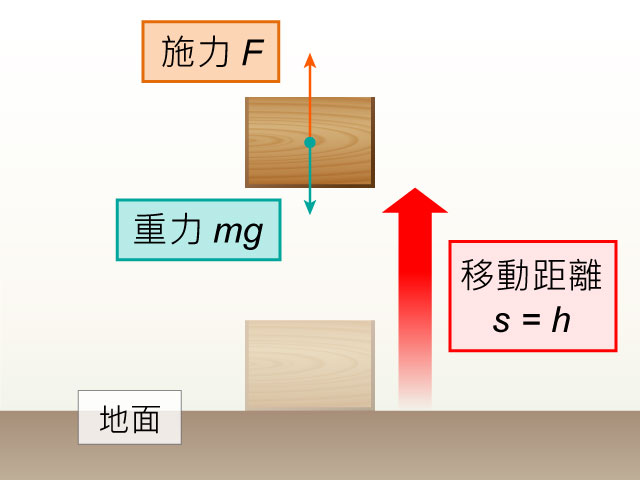
接下來我們嘗試推導重力勢能的表達式。設對質量為 \(m\) 的物體作用一垂直恆力 \(F\)，令其以勻速率沿垂直方向從離地高度為 \({{y}_{1}}\) 的位置移動至離地更高的位置 \({{y}_{2}}\)，即 \({{y}_{1}}\) < \({{y}_{2}}\)。考慮 \(F\) 對物體的作功 \({{W}_{F}}\) = \(F\) (\({{y}_{2}}\) − \({{y}_{1}}\))；而重力的作功為負功，所以 \({{W}_{mg}}\) = −\(mg\) (\({{y}_{2}}\) − \({{y}_{1}}\))。由於物體以勻速運動，\(F\) = \(mg\)，換言之：

施力的作功   \({{W}_{F}}\) = \(mg\)\({{y}_{2}}\) − \(mg\)\({{y}_{1}}\)
重力的作功   \({{W}_{mg}}\) = \(mg\)\({{y}_{1}}\) − \(mg\)\({{y}_{2}}\)

式中 “\(mgy\)” 就是重力勢能、而 “\(mg\)\({{y}_{2}}\) − \(mg\)\({{y}_{1}}\)” 是重力勢能的變化，即重力勢能從 \(mg\)\({{y}_{1}}\) 轉變為 \(mg\)\({{y}_{2}}\)。留意上式亦適用於物體向下移的情況的，即 \({{y}_{1}}\) > \({{y}_{2}}\)。針對情境的話：\({{y}_{1}}\) = 0、\({{y}_{2}}\) = \(h\)，即施力與重力的作功分別是：

由此顯示，如果 Δ\(U\) 代表重力勢能的變化，重力對物體的作功：