之前我們學習過功的概念,曾指出功是能量變化或轉移的量度。現在我們再看能量這概念,可進一步說明:
能量 \(=\) 對物體作功的能力
換言之,要測量能量的多寡時,便要測量其作功的量。物體具有能量,便表示擁有對其他物體作功的能力。例如打桌球時(),我們用球桿推白色球,令其加速撞擊靜止的 8 號球。造成白球推動 8 號球移向前。顯然,對 8 號球作功的就是正在運動的白球。事實上,對於擁有運動速率的物體、藉運動而具有作功的能力(即能量),我們稱這種能量為動能 (kinetic energy):
動能為物體因其運動而擁有的能量。
從更仔細實驗中可進一步觀察到,運動的物體速度愈大、動能愈大;質量愈大、動能也愈大。至於靜止中的物體要獲得動能,則須藉外力對其作功,就如中的 8 號球因白球對其作功,於碰撞後獲得動能。
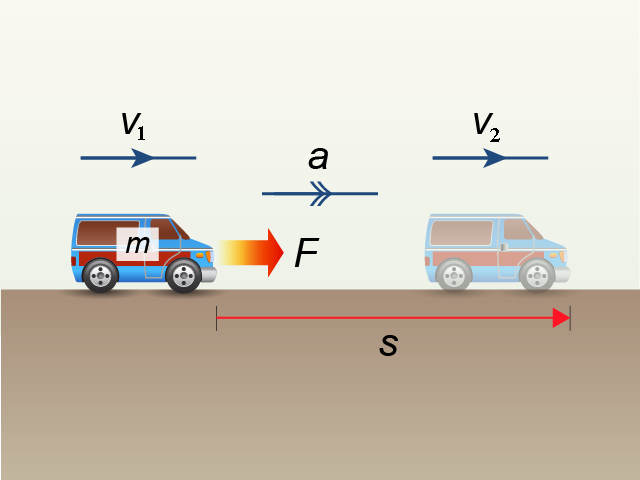
要推導動能的表達式,我們可以利用這情境以作說明。
一輛質量為 \(m\) 的車子於水平地面上運動中。由引擎提供的恆力 \(F\),持續作用於車子的運動方向,令車子於經過了位移變化 \(s\) 的前後、速率從 \({{v}_{1}}\) 變為 \({{v}_{2}}\)(忽略空氣阻力與來自地面的摩擦力)。根據牛頓第二定律與勻加速運動方程,分別可寫出:
\(F\) = \(m\) \(a\) \({{v}_{2}}^{2}\) − \({{v}_{1}}^{2}\) = 2 \(a\) \(s\)
符號 \(a\) 是車子的加速度。合併兩式以消去 \(a\) 得:
\(\displaystyle{Fs=\frac{1}{2}m{{v}_{2}}^{2}-\frac{1}{2}m{{v}_{1}}^{2}}\)
先留意上式右方,一個「\(\tfrac{1}{2}m{{v}^{2}}\) 格式」、屬過程末的能量,減去另一個同為「\(\tfrac{1}{2}m{{v}^{2}}\) 格式」、屬過程初的能量,剛好等於恆力 \(F\) 的作功 (\(Fs\))!似乎「\(\tfrac{1}{2}m{{v}^{2}}\)」乃存在特別意義的物理量。這個量跟物體的速率有關,那便與物體源於獲得運動速率而具有動能這理解一致。於是,人們把質量為 \(m\) 的物體以速率 \(v\) 運動時的動能,定義作 \(\tfrac{1}{2}m{{v}^{2}}\),慣常以 \(K\) 或 \(KE\) 等符號表示:
動能 \(\displaystyle KE=\frac{1}{2}m{{v}^{2}}\)
動能是標量,它的國際單位制單位與功相同,都是焦耳,簡寫為 \(\text{J}\)。
歸納一下這情況就是:\(F\) 對車子作功 (\(W\)),造成有能量轉移給車子,車子出現動能變化。若稱 \(\tfrac{1}{2}m{{v}_{1}}^{2}\) 和 \(\tfrac{1}{2}m{{v}_{2}}^{2}\) 分別為車子的始動能和末動能,即: