試想像，一件置於粗糙地面上的物體被拖動時，作用於物體上的力會包括：我們施加的拖力、物體的重量、地面給物體的摩擦力和承托力。換言之，對該物體作功的力，除了我們給物體的拖力外，還有摩擦力（重量與承托力垂直於物體位移故不作功）。

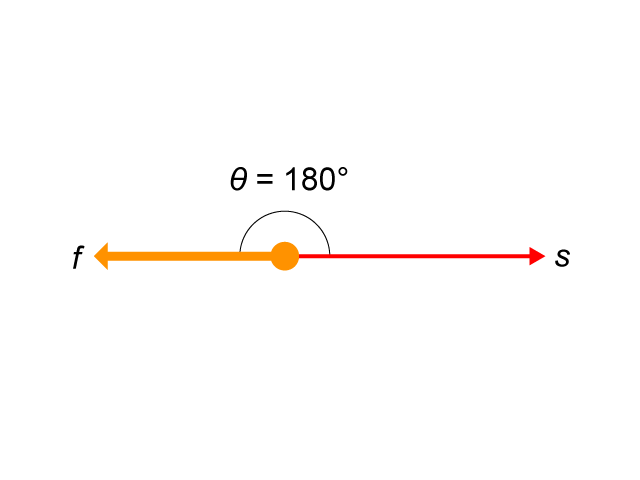
作為說明，試考慮在粗糙水平地面上，一傾斜恆力 \(T\) 作用於紙箱上，令紙箱沿地面運動而造成位移 \(s\)（見）。如果 \(T\) 與 \(s\) 之間的角設為 \(\phi \)，\(T\) 對紙箱的作功就是 \(Ts\) \(\cos \phi \)。至於摩擦力 \(f\)，設其與 \(s\) 之間的角為 \(\theta \)。由於摩擦力跟紙箱運動的方向相反，因此，\(f\) 與位移之間的角度是 \(180^ \circ \)（見）。應用功的表達式：\(W=fs\ \cos \theta \)，摩擦力對紙箱的作功便寫成：

在本情境，\(T\) 對紙箱作正功 (\(\because \cos \phi \) > 0)、摩擦力對紙箱作負功 (\(\because \cos \theta \) < 0)，後者也可以說成「紙箱克服摩擦力的作功」。留意功的正負並非表示功有方向性，而是反映其令物體能量的增減。綜合而言：

如中摩擦力的作功便會令能量從紙箱轉移往他處。

水平車道上，一輛行駛中的汽車突然煞車，在路面上滑行了 \(0.7 \text{ m}\) 的距離。假使在煞車過程中，輪胎和地面之間有 \(1300 \text{ N}\) 的恆定摩擦力，過程中摩擦力的作功是多少？

【題解】

設 \(f\) 和 \(s\) 分別代表摩擦力與制動過程中的位移，兩者的方向相反，如中所示。摩擦力的作功就是：

\(W=fs\ \cos \theta \)

式中 \(\theta \) 代表 \(f\) 與 \(s\) 之間的夾角。代入數字：

\(W=\left( 1300\ \text{N} \right)\left( 0.7\ \text{m} \right)\cos 180{}^\circ \)

運算後得 \(W\) = \(-910\text{ J}\)。換言之，摩擦力作功的大小為 \(910\text{ J}\)。