當物體以固定的正加速度運動,有關的速度-時間關係線圖(\(v\)-\(t\) 線圖)是怎樣的呢?
你可打開下方內容,根據指示利用「運動與線圖模擬程式」繪畫車子的 \(v\)-\(t\) 線圖,再演示車子的運動:
請嘗試用模擬程式,找出下列哪些 \(v\)-\(t\) 線圖代表物體以固定的正加速度運動?
(a)
(b)
(c)
(d)
【題解】 物體以固定的正加速度運動,表示 \(a > 0\),並為一常數。換言之,(a)、(c) 和 (d) 均代表物體以固定的正加速度運動,它們的分別僅為各自有不同的初速度((a)、(c) 和 (d) 分別為 \(u > 0\)、\(u = 0\) 和 \(u < 0\))。
你也可以在運動與線圖模擬程式按(a) 至 (d) 繪畫,再演示車子運動,驗證車子是否進行勻加速運動。例如一條呈水平線的 \(a\)-\(t\) 線圖,其 \(v\)-\(t\) 線圖便是一條遞增的直線,表示物體均勻地加速向右運動。
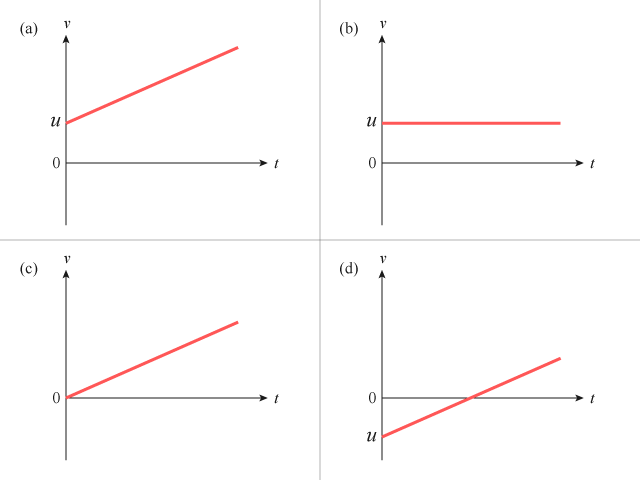
考慮一個物體以 \(−1 \text{ m}\ {{\text{s}}^{-2}}\) 的固定加速度運動,運動並持續了 \(15 \text{ s}\)。若該物體在 \(0 \text{ s}\) 的速度等於 \(10 \text{ m}\ {{\text{s}}^{-1}}\),試用鼠標把右方的線段放在圖上的正確位置,繪畫物體從 \(0\) 至 \(15 \text{ s}\) 的 \(v\)-\(t\) 線圖。
按著線中央可移動圖線,按著線的末端可改變其方位和長度。完成後請按「提交」。
根據活動的結果,請在下方選擇正確的項目:
【題解】 顯示以固定的負加速度運動的三種 \(v\)-\(t\) 線圖。(a)、(b) 和 (c) 分別是初速度 \(u > 0\)、\(u = 0\) 和 \(u < 0\) 的情況。
試在模擬程式輸入 \(v\)-\(t\) 線圖後,再按「播放」演示運動吧!
可以如何從 \(v\)-\(t\) 線圖求物體的加速度呢?
在「函數與圖像模擬程式」中,程式會根據 \(f\left( t \right)\) 所定義的方程繪畫圖像。你可打開下方內容,根據指示利用模擬程式探究一條直線的方程:
考慮勻加速運動方程:\(v=u+a\ t\),將它與上方活動的結果比較,可知:
【題解】 「直線方程格式」活動的結果顯示,一條直線的方程為:
\(f\left( t \right)=c+m\ t\)
上式與 \(v=u+a\ t\) 比較,可知 \(a\) 等於 \(v\)-\(t\) 線圖中的斜率。
上方假設了物體進行勻加速運動,若 \(a\) 並非固定,關係 (1) 仍成立嗎?
未能掌握「\(a\ne \) 常數」的意義?下方會討論非勻加速運動的線圖性質:
記得上一節討論勻速運動 \(v\)-\(t\) 線圖時,有以下結論:
物體進行勻速運動時(\(a\) = 0),\(v\)-\(t\) 線圖下的面積等於位移變化。
這結果會同樣適用於勻加速運動嗎?
若把 \(v\)-\(t\) 線圖分成多個極短的時段,每個時段內的速度固定不變。考慮每個時段的位移計算,然後把所有時段的位移加起來,可得以下關係:
位移的變化 \(\Delta s\) = \(v\)-\(t\) 線圖下的面積
這相當於在的模擬程式中,當 \(n\) 愈大,黃色區域的面積愈接近線圖下的面積。
換言之,以上這個關係同時適用於勻速與勻加速運動。
在之前的學習中,已定義過速度和加速度:
\(\displaystyle{v=\frac{\delta s}{\delta t}}\)
\(\displaystyle{a=\frac{\delta v}{\delta t}}\)
另在學習「速度-時間關係線圖」時,得到結果:
\(v\)-\(t\) 線圖下的面積 = 位移的變化 \(\Delta s\)
那麼,或可由以上關係推斷,\(a\)-\(t\) 線圖下的面積有何意義嗎?
【題解】 考慮「\(v={\delta s}/{\delta t}\;\)」和「位移變化 \(\Delta s\) = \(v\)-\(t\) 線圖下面積」分別表示:
從 \(s\)-\(t\) 線圖計算斜率可得速度 \(v\); 從 \(v\)-\(t\) 線圖計算圖下面積得回位移變化 \(\Delta s\)。
由於「\(a={\delta v}/{\delta t}\;\)」表示:
從 \(v\)-\(t\) 線圖計算斜率可得加速度 \(a\);
換言之,方程 (2) 可類別為:
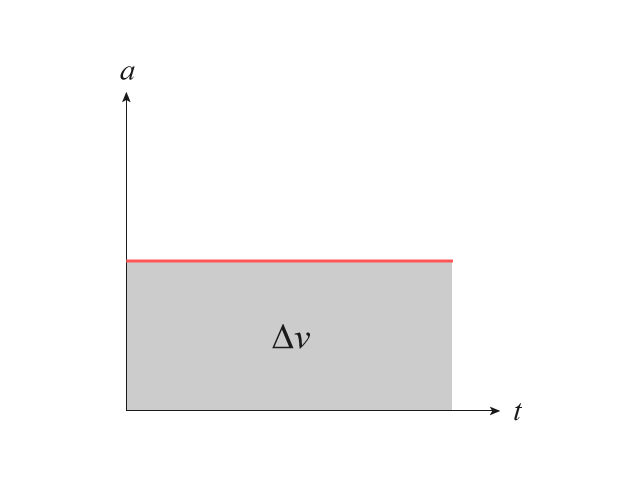
從 \(a\)-\(t\) 線圖計算圖下面積得回速度變化 \(\Delta v\)。
在勻加速運動中,位移-時間 (\(s\)-\(t\)) 關係線圖是什麼圖像來呢?
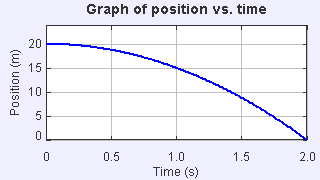
如考慮一個小球從海拔 \(20 \text{ m}\) 釋放,忽略空氣阻力的話,小球在重力的作用下會進行勻加速運動(自由落體)。右方的「垂直運動模擬程式 \(1\)」可模擬一個小球的垂直運動,我們可以藉模擬程式探究勻加速運動 \(s\)-\(t\) 線圖。由此可知:
【題解】 小球的 \(s\)-\(t\) 線圖是一條拋物線(見)。線圖顯示小球會於釋放後 \(2 \text{ s}\) 到達地面。
【例子】一個物體以 \(−2 \text{ m}\ {{\text{s}}^{-2}}\) 的固定加速度運動。若該物體的初速度與始位移分別是 \(20 \text{ m}\ {{\text{s}}^{-1}}\) 和 \(−75 \text{ m}\)。請寫出物體在時間 \(t\) 等於 \(5 \text{ s}\)、\(10 \text{ s}\) 和 \(15 \text{ s}\) 時的速度:
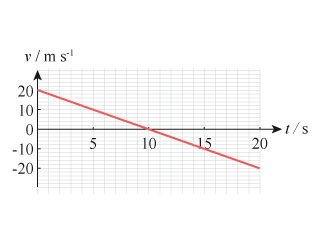
【題解】 已知 \(a = −2 \text{ m}\ {{\text{s}}^{-2}}\)、\(u = 20 \text{ m}\ {{\text{s}}^{-1}}\)、\({{s}_{0}} = −75 \text{ m}\)。考慮 \(v=u+a\ t\),得:
\(v=20-2\ t\)
分別把時間代入上式,可知在 \(5 \text{ s}\) 和 \(15 \text{ s}\) 時的速度分別是 \(10 \text{ m}\ {{\text{s}}^{-1}}\) 和 \(−10 \text{ m}\ {{\text{s}}^{-1}}\)。而 \(10 \text{ s}\) 時的速度是 \(0\)。顯示物體的 \(v\)-\(t\) 線圖。
記得速度的定義為 \(v={\delta s}/{\delta t}\;\),換言之:
速度 \(v\) = \(s\)-\(t\) 線圖中的斜率