在勻速運動中,若我們把物體速度對時間的關係繪成圖表(稱為 \(v\)-\(t\) 線圖),有關的線圖是怎樣的呢?
你可打開下方內容,根據指示利用「運動與線圖模擬程式」移動車子,繪畫車子運動的 \(v\)-\(t\) 線圖:
試從模擬結果探究勻速運動 \(v\)-\(t\) 線圖,在下方選擇正確的項目:
【題解】 在勻速運動中,\(v\)-\(t\) 線圖是一條水平的直線,下圖顯示物體在固定速度下運動的 \(v\)-\(t\) 線圖:
你也可以在運動與線圖模擬程式先繪出 \(v\)-\(t\) 線圖,再演示車子的運動。

根據勻速運動的關係式:
\(s={{s}_{0}}+v\ t\)
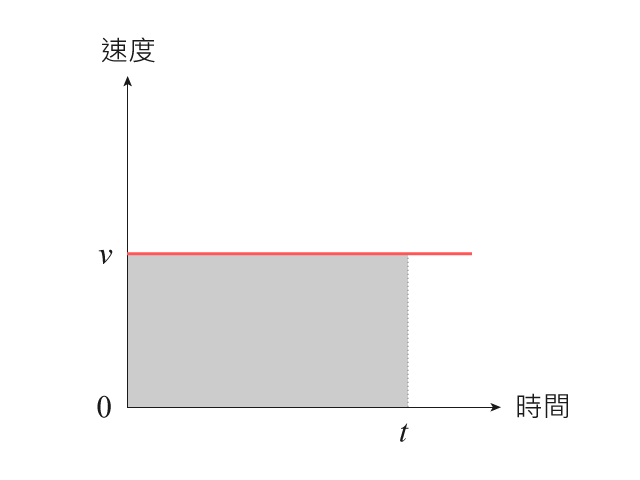
另一方面,在的勻速運動 \(v\)-\(t\) 線圖,考慮時間從 \(0\) 至 \(t\),可知圖線下的面積(灰階部分)為:
【題解】 灰階部分為矩形,面積 \(= v\ t\)。
比較勻速運動關係式與上方的結果,可知:
【題解】 由於位移 \(s={{s}_{0}}+v\ t\) = \({{s}_{0}}\) +(\(v\)-\(t\) 線圖下面積)
\(\begin{align}\Rightarrow v\text{-}t \text{ 線圖下面積} &= s - {{s}_{0}} \\ &= \text{位移的變化}\end{align}\)
若考慮一個質點從原點開始以 10 \(\text{m}\ {{\text{s}}^{-1}}\) 的速度運動並持續了 5 \(\text{s}\)。接着,物體的速度突然變為 −5 \(\text{m}\ {{\text{s}}^{-1}}\),之後在這速度維持了 10 \(\text{s}\) 的運動。
試用鼠標把右方的線段放在圖內的正確位置,繪畫質點的 \(v\)-\(t\) 線圖。按著線中央可移動圖線,按著線的末端可改變其方位和長度。完成後請按「提交」。根據的結果,請計算該質點的下列各項物理量:
【題解】 位移變化乃 \(v\)-\(t\) 線圖下面積,考慮:
從 \(t = 0\) 至 \(5 \text{ s}\),\(\text{位移變化} = 5 \times 10 \text{ m} = 50 \text{ m}\) 從 \(t = 5\) 至 \(15 \text{ s}\),\(\text{位移變化} = −5 \times 10 \text{ m} = −50 \text{ m}\)
換言之,\(t = 0\) 至 \(15 \text{ s}\) 的位移變化 \(= 0 \text{ m}\),物體最終回到原點。
行走距離為 \(0\) 至 \(5 \text{ s}\) 與 \(5\) 至 \(15 \text{ s}\) 兩段行走距離的總和:
\(t = 0\) 至 \(15 \text{ s}\) 的行走距離 \(= 100 \text{ m}\)
你也可以在運動與線圖模擬程式先繪出 \(v\)-\(t\) 線圖,驗證你的答案。
【題解】 \(\begin{align}\text{平均速率} &= \text{總行走距離 / 時間} \\ &= 100 \text{ m} / 15 \text{ s} \\ &= 6.7 \text{ m}\ {{\text{s}}^{-1}}\end{align}\)
\(\begin{align}\text{平均速度} &= \text{位移變化 / 時間} \\ &= 0 \text{ m} / 15 \text{ s} \\ &= 0 \text{ m}\ {{\text{s}}^{-1}}\end{align}\)
在勻速運動中,若把位移對時間的關係繪成圖表(稱為 \(s\)-\(t\) 線圖),有關線圖是怎樣呢?
你可打開下方內容,根據指示利用「運動與線圖模擬程式」移動車子,繪畫車子運動的 \(s\)-\(t\) 線圖(已設向右為正):
根據模擬結果探究勻速運動 \(s\)-\(t\) 線圖,可知中哪些是勻速運動的 \(s\)-\(t\) 關係線圖?
(a)
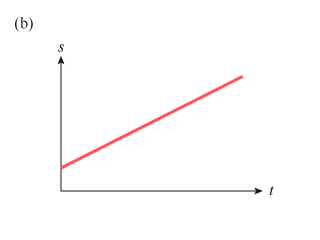
(b)
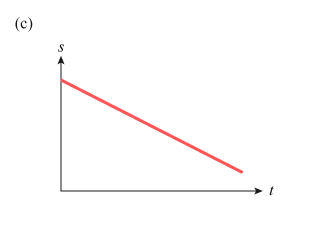
(c)
【題解】 (a) 顯示物體的位移隨時間固定不變。
(b) 與(c) 顯示物體的位移均勻地隨時間遞增或遞減,兩幅圖也是勻速運動的 \(s\)-\(t\) 線圖。
你也可以在運動與線圖模擬程式按(a) 至(c) 繪畫,然後按「播放」演示車子運動,驗證你的答案。
請在下方選擇正確的答案:
(b) 的 \(s\)-\(t\) 線圖顯示車子 運動;
【題解】 在運動與線圖模擬程式中,已假設向右為正,所以
遞增的位移表示物體向右運動; 遞減的位移表示物體向左運動。
根據勻速運動的關係式:
\(s={{s}_{0}}+v\ t\)
要描述一條直線時,可使用斜截式方程:
\(y=m\ x+c\)
比較上式與勻速運動關係式,可知勻速運動中,\(s\)-\(t\) 線圖中的斜率等於:
【題解】 實際上,我們在之前的學習已知速度的定義等於
\(\displaystyle{v=\frac{\Delta s}{\Delta t}}\)
而 \({\Delta s}/{\Delta t}\;\) 就即是直線在 \(s\)-\(t\) 圖上的斜率,所以 \(s\)-\(t\) 線圖的斜率就是速度。
在(b) 與(c),你能決定有關物體的速度大於零、小於零、還是等於零嗎?
(b) 所代表的物體的速度 ;
【題解】 (b) 的斜率為正,表示速度大於零,所以物體向右移;
(c) 的斜率為負,表示速度小於零,所以物體向左移。
總括而言,若某物體運動的 \(s\)-\(t\) 線圖為已知,我們可以從 \(s\)-\(t\) 線圖計算出相應的 \(v\)-\(t\) 線圖。


所示為某物體的 \(s\)-\(t\) 線圖。我們可以根據線圖,來描述該物體的運動。你也可以根據,在運動與線圖模擬程式繪畫 \(s\)-\(t\) 線圖。
請在下方的空格上選擇正確的項目:
物體的起始位移等於 \(\text{m}\)。
【題解】 由於顯示當 \(t = 0\),\(s = −10 \text{ m}\),所以物體的起始位移等於 \(−10 \text{ m}\)。
在圖線與時間軸相交(即 \(s = 0\))的時間,物體便位於原點。根據,當 \(t = 5 \text{ s}\) 與 \(15 \text{ s}\),物體均位於原點。
\(s\)-\(t\) 線圖的斜率就是速度,我們可以藉計算物體的 \(v\)-\(t\) 圖,得:
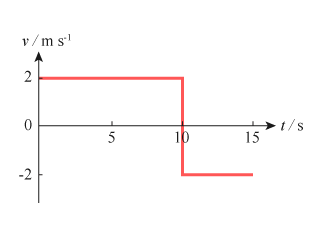
留意當 \(t\) 從 \(0\) 至 \(10 \text{ s}\),\(v = 2 \text{ m}\ {{\text{s}}^{-1}}\);當 \(t\) 從 \(10\) 至 \(15 \text{ s}\),\(v = −2 \text{ m}\ {{\text{s}}^{-1}}\)。
【題解】 物體的起始位移與最終位移分別是 \(−10 \text{ m}\) 和 \(0 \text{ m}\),所以:
\(\begin{align}\text{位移變化} &= \text{最終位移} − \text{起始位移} \\ &= 0 \text{ m} − (−10 \text{ m}) \\ &= 10 \text{ m}\end{align}\)
\(\begin{align}\text{平均速度} &= \text{位移變化 / 時間} \\ &= 10 \text{ m} / 15 \text{ s} \\ &= 0.67 \text{ m}\ {{\text{s}}^{-1}}\end{align}\)
物體從 \(t = 0\) 至 \(10 \text{ s}\),朝同一方向行走了 \(20 \text{ m}\);而從 \(t = 10\) 至 \(15 \text{ s}\),則朝相反方向行走了 \(10 \text{ m}\)。換言之:
\(\begin{align}\text{總行走距離} &= 20 \text{ m} + 10 \text{ m} \\ &= 30 \text{ m}\end{align}\)
\(\begin{align}\text{平均速率} &= \text{總行走距離 / 時間} \\ &= 30 \text{ m} / 15 \text{ s} \\ &= 2 \text{ m}\ {{\text{s}}^{-1}}\end{align}\)