當一個物體被釋放或拋出時,由於地球重力的作用,物體便會有加速度。
顯示一個直徑 \(5 \text{ cm}\) 的塑膠小球從海拔 \(80 \text{ m}\) 釋放。結果顯示:
【題解】 質量較大的球應同樣花 \(4 \text{ s}\) 到達水面,小球質量的多寡不會影響其到達水平面所費的時間。
實際上,在忽略空氣阻力的情況下,在同一地點、同等高度釋放不同質量或不同形狀的物體,它們下墜所花的時間均沒有差別。
在上方的例子中,有關垂直運動為自由落體 (free fall) 的情況,就是不考慮空氣阻力、摩擦力等效應,只有重力 (gravity) 作用在物體時的情況。
日常生活中,物體在空氣中運動就會受到空氣阻力的影響。你可根據下方的指示加上空氣阻力的效應,觀察物體的垂直運動:
設 \({{a}_{1}}\) 與 \({{a}_{2}}\) 分別是例子中,使用質量較小和較大的球進行試驗所得的小球加速度。試在垂直運動模擬程式 \(2\) 設置 \({{\rho }_{air}}=0\) 以排除空氣阻力,觀察不同質量小球在下墜過程中的加速度,找出下方正確的敘述:
(1)\({{a}_{1}}\) 的量值較 \({{a}_{2}}\) 的小
(2)\({{a}_{1}}\) 與 \({{a}_{2}}\) 的方向在過程中維持不變
(3)\({{a}_{1}}\) 的量值約等於 \(10 \text{ m}\ {{\text{s}}^{-2}}\),過程中維持不變
【題解】 在自由落體的情況,所有物體在同一地點、相同海拔高度的加速度是相同的,這加速度作用於所有的物體上,稱為重力加速度 (gravitational acceleration),通常以符號 \(g\) 表示。
在地球表面,重力加速度的量值約等於 \(9.8 \text{ m}\ {{\text{s}}^{-2}}\),所以 \(a\)-\(t\) 線圖是一條水平的直線。為計算方便,有時會取近似值 \(10 \text{ m}\ {{\text{s}}^{-2}}\)。
那麼,在月球表面的垂直運動是如何的呢?垂直運動模擬程式 \(1\) 中的線圖顯示了小球位移、速度和加速度隨時間的變化。試在模擬程式設置 \(g = 1.7 \text{ m}\ {{\text{s}}^{-2}}\),模擬月球表面的重力加速度。
當考慮一個物體在重力的作用下自由下落,習慣上我們會設向上為正速度的方向。那麼,自由落體的加速度方向是怎麼樣的?
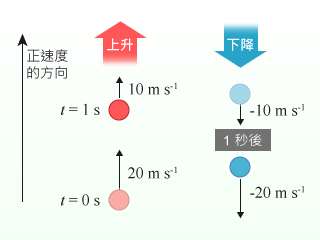
假定的下墜自由落體運動為情況 \(1\),我們再考慮以 \(40 \text{ m}\ {{\text{s}}^{-1}}\) 把小球上拋(),定為情況 \(2\)。根據加速度的定義或模擬程式的結果,兩情況的加速度方向:
【題解】 在情況 \(2\),先考慮小球向上運動的一程。如附圖的紅色小球,它的速度正在減少(每秒減少 \(10 \text{ m}\ {{\text{s}}^{-1}}\))。換言之,根據加速度定義 \(a = \Delta v\) / \(\Delta t\),可知 \(a\) 小於 \(0\),即 \(−10 \text{ m}\ {{\text{s}}^{-2}}\)。
當球到達最高點,小球運動瞬間靜止,方向會由向上轉為向下,之後轉為向下運動。如圖的藍色小球所示,其速度正在減少(留意 \(−20 \text{ m}\ {{\text{s}}^{-1}} < −10 \text{ m}\ {{\text{s}}^{-1}}\),但速率正在增加),所以加速度是負,即 \(−10 \text{ m}\ {{\text{s}}^{-2}}\)。
在情況 \(1\),小球從靜止下墜,情況相當於情況 \(2\) 中向下運動的一程,所以加速度是負,即 \(−10 \text{ m}\ {{\text{s}}^{-2}}\)。結論為不論是下墜(情況 \(1\))還是上拋(情況 \(2\))的自由落體運動,重力加速度的方向垂直向下。
留意:
試完成下方的問題,鞏固有關自由落體運動的概念掌握:
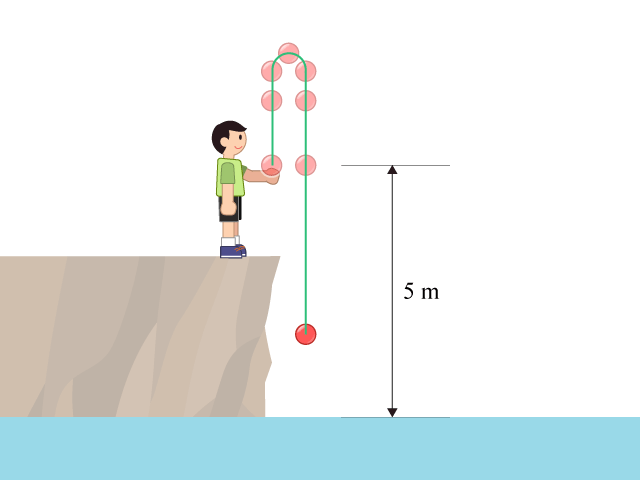
【問題 \(1\)】將一石塊在離水面 \(5 \text{ m}\) 高的位置以 \(20 \text{ m}\ {{\text{s}}^{-1}}\) 的速率往上拋。石塊到達最高點後改為下墜。求石塊到達最高點需時多久?(設重力加速度為 \(10 \text{ m}\ {{\text{s}}^{-2}}\))
A. \(1.0 \text{ s}\)
B. \(1.5 \text{ s}\)
C. \(2.0 \text{ s}\)
【題解】 石塊到達最高點時速度等於零。設向上為正,應用勻加速運動方程:
\(v=u+a\ t\) \(0=20\ \text{m}\ {{\text{s}}^{-1}}+\left( -10\ \text{m}\ {{\text{s}}^{-2}} \right)\ t\) \(\Rightarrow t=2\ \text{s}\)
留意設向上為正時,\(a = −g = −10 \text{ m}\ {{\text{s}}^{-2}}\)。
【問題 \(2\)】石塊到達水面時的速率為多少?
A. \(10 \text{ m}\ {{\text{s}}^{-1}}\)
B. \(22 \text{ m}\ {{\text{s}}^{-1}}\)
C. \(36 \text{ m}\ {{\text{s}}^{-1}}\)
【題解】 設向上為正,石塊到達水面時的速度為:
\(\begin{align}{{v}^{2}}-{{u}^{2}} &= 2a\ s \\ {{v}^{2}}-{{\left( 20\ \text{m}\ {{\text{s}}^{-1}} \right)}^{2}} &= 2\left( -10\ \text{m}\ {{\text{s}}^{-2}} \right)\left( -5\ \text{m} \right) \\ v &= -22.4\ \text{m}\ {{\text{s}}^{-1}}\end{align}\)
留意位移 \(s\) 取負數,因為石塊到達水面時,它位於拋出位置之下。
【問題 \(3\)】石塊到達水面時已行走了多長距離?
A. \(5 \text{ m}\)
B. \(20 \text{ m}\)
C. \(40 \text{ m}\)
D. \(45 \text{ m}\)
【題解】 先求石塊到達最高點時的位移:
\(\begin{align}{{v}^{2}}-{{u}^{2}} &= 2a\ s \\ 0-{{\left( 20\ \text{m}\ {{\text{s}}^{-1}} \right)}^{2}} &= 2\ \left( -10\ \text{m}\ {{\text{s}}^{-2}} \right)\ s \\ s &= 20\ \text{m}\end{align}\)
若在垂直運動模擬程式設定有關運動,可觀察到石塊先上升 \(20 \text{ m}\),然後下墜 \(20 \text{ m}\) 至起始高度,之後再下落 \(5 \text{ m}\) 至水面。換言之,行走距離為 \(2 \times 20 \text{ m} + 5 \text{ m}\),等於 \(45 \text{ m}\)。