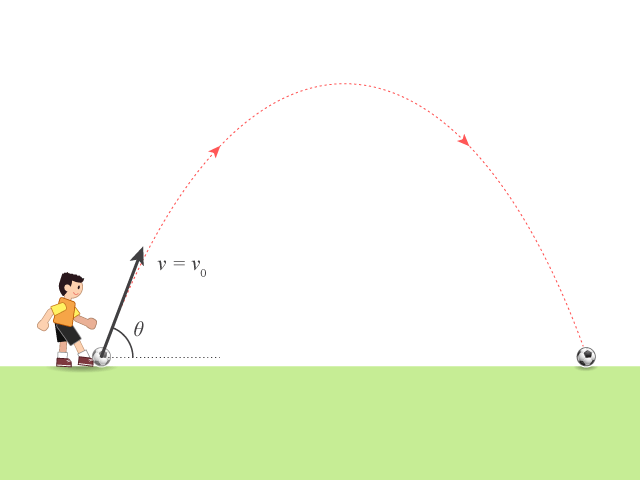
飛行時間 (time of flight) 是拋體從拋出直至着地所經過的時間。
設向上為正、\({{v}_{0}}\) 與 \(\theta \) 分別為初速度的量值和方向,一個進行斜拋運動的物體,其垂直方向的位移是:
\(\displaystyle{{{s}_{y}}={{v}_{0}}t\sin \theta -\frac{1}{2}g\ {{t}^{2}}}\)
在的情況,拋體在同一水平被拋出和着地,換言之,在上式設 \({{s}_{y}}=0\),得飛行時間 \({{t}_{f}}\) 為:
\(\displaystyle{{{t}_{f}}=\frac{2{{v}_{0}}\sin \theta }{g}}\)
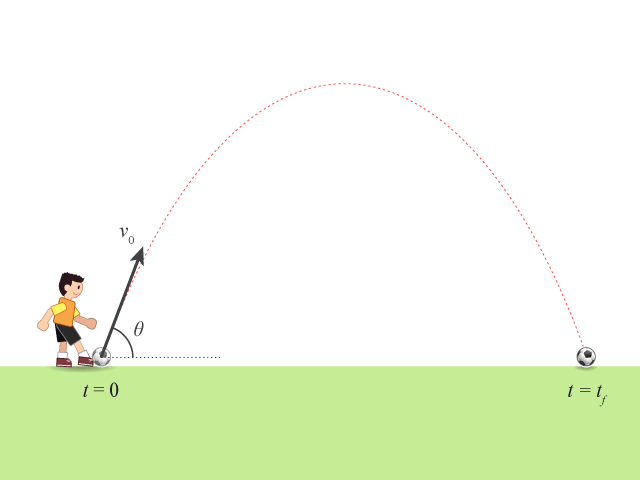
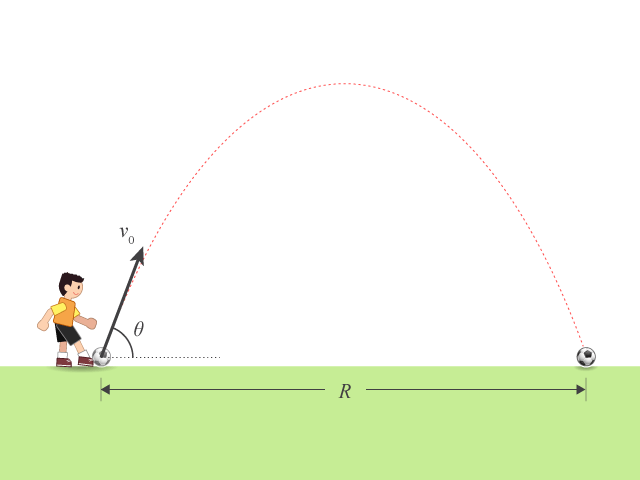
射程 (range) 是拋體在水平方向上所飛行的距離。
設向上為正、\({{v}_{0}}\) 與 \(\theta \) 分別為初速度的量值和方向,一個進行斜拋運動的物體,其水平與垂直方向的位移分別是:
\(\displaystyle{{{s}_{x}}={{v}_{0}}t\cos \theta }\) ---------- (1)
\(\displaystyle{{{s}_{y}}={{v}_{0}}t\sin \theta -\frac{1}{2}g\ {{t}^{2}}}\) ---------- (2)
在的情況,拋體在同一水平被拋出和着地,換言之,在方程 (2) 設 \({{s}_{y}}=0\),得飛行時間為:
\(\displaystyle{t=\frac{2{{v}_{0}}\sin \theta }{g}}\)
把上式代入方程 (1),得拋體的射程(以 \(R\) 表示)為:
\(\displaystyle{R=\frac{{{v}_{0}}^{2}\sin 2\theta }{g}}\)
留意當 \(\sin 2\theta =1\),拋體的射程達至最大值。這相當於 \(\theta =45{}^\circ \)。
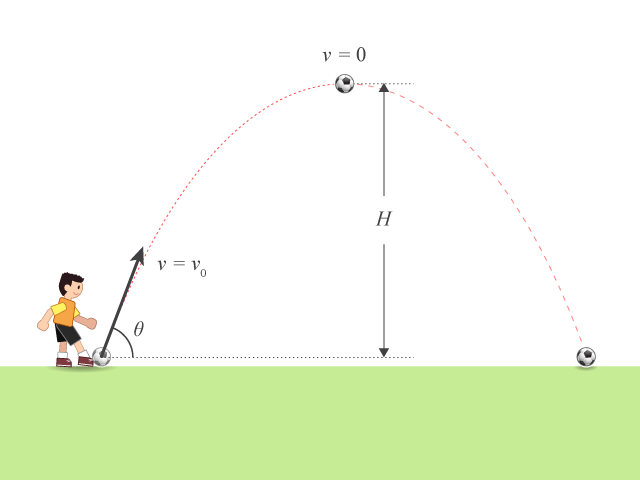
拋體的垂直速度變為零時,拋體便到達其最大高度 (maximum height)。
設向上為正、\({{v}_{0}}\) 與 \(\theta \) 分別為初速度的量值和方向,一個進行斜拋運動的物體,其垂直方向的速度和位移分別是:
\({{v}_{y}}={{v}_{0}}\sin \theta -g\ t\) ---------- (1)
\(\displaystyle{{{s}_{y}}={{v}_{0}}t\sin \theta -\frac{1}{2}g\ {{t}^{2}}}\) ---------- (2)
在方程 (1) 設 \({{v}_{y}}=0\),得拋體到達其最大高度時的時間:
\(\displaystyle{t=\frac{{{v}_{0}}\sin \theta }{g}}\)
留意這時間剛好是飛行時間的一半,表示拋體在最高點兩邊的運動左右對稱。把上式代入方程 (2),得拋體的最大高度(以 \(H\) 表示)為:
\(\displaystyle{H=\frac{{{v}_{0}}^{2}{{\sin }^{2}}\theta }{2g}}\)
軌道 (trajectory) 用來描述拋體運動的路徑。
設向上為正、\({{v}_{0}}\) 與 \(\theta \) 分別為初速度的量值和方向,一個進行斜拋運動的物體,其水平和垂直方向的位移分別是:
\(\displaystyle{{{s}_{x}}={{v}_{0}}t\cos \theta }\) ---------- (1)
\(\displaystyle{{{s}_{y}}={{v}_{0}}t\sin \theta -\frac{1}{2}g\ {{t}^{2}}}\) ---------- (2)
合併方程 (1) 和 (2) 以消去 \(t\),可以得到一條描述斜拋體的軌道的方程(見):
\(\displaystyle{{{s}_{y}}={{s}_{x}}\tan \theta -\frac{g}{2{{v}_{0}}^{2}{{\cos }^{2}}\theta }{{s}_{x}}^{2}}\)
留意上式為一條拋物線方程。