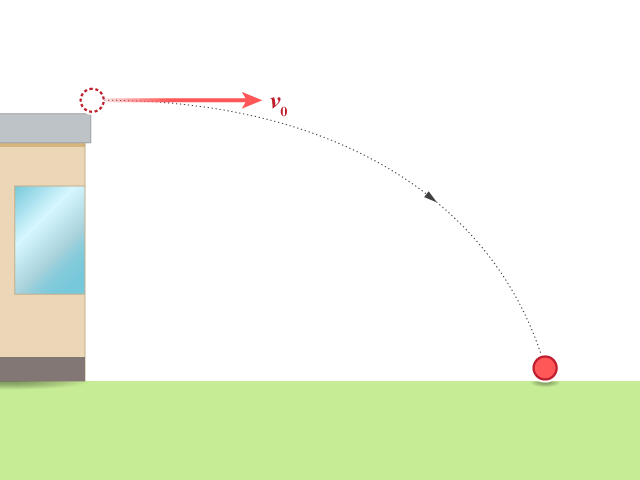
飛行時間 (time of flight) 是拋體從拋出直至着地所經過的時間。
設向上為正、\({{v}_{0}}\) 為初速度(沿水平方向),一個進行平拋運動的物體,其垂直方向的位移是:
\(\displaystyle{{{s}_{y}}=-\frac{1}{2}g\ {{t}^{2}}}\)
在的情況,拋體在距離地面高度為 \(h\) 的屋頂上被拋出,換言之,在上式設 \({{s}_{y}}=-h\),得飛行時間 \({{t}_{f}}\) 為:
\(\displaystyle{{{t}_{f}}=\sqrt{\frac{2h}{g}}}\)
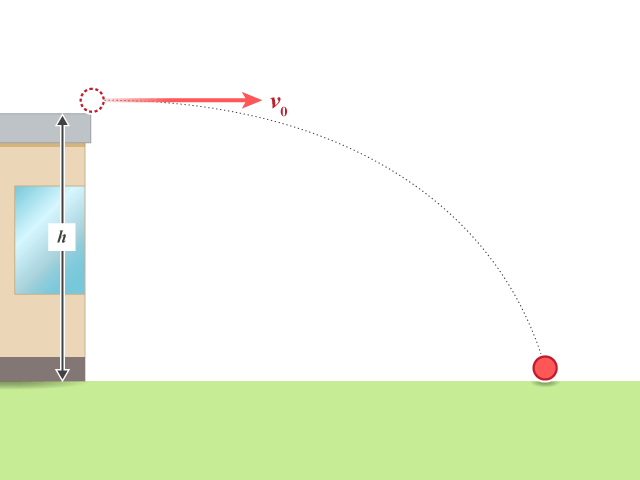
射程 (range) 是拋體在水平方向上所飛行的距離。
設向上為正、\({{v}_{0}}\) 為初速度(沿水平方向),一個進行平拋運動的物體,其水平與垂直方向的位移分別是:
\({{s}_{x}}={{v}_{0}}t\) ---------- (1)
\(\displaystyle{{{s}_{y}}=-\frac{1}{2}g\ {{t}^{2}}}\) ---------- (2)
在的情況,拋體在距離地面高度為 \(h\) 的屋頂上被拋出,換言之,在方程 (2) 設 \({{s}_{y}}=-h\),得飛行時間為:
\(\displaystyle{t=\sqrt{\frac{2h}{g}}}\)
把上式代入方程 (1),得拋體的射程(以 \(R\) 表示)為:
\(\displaystyle{R={{v}_{0}}\sqrt{\frac{2h}{g}}}\)
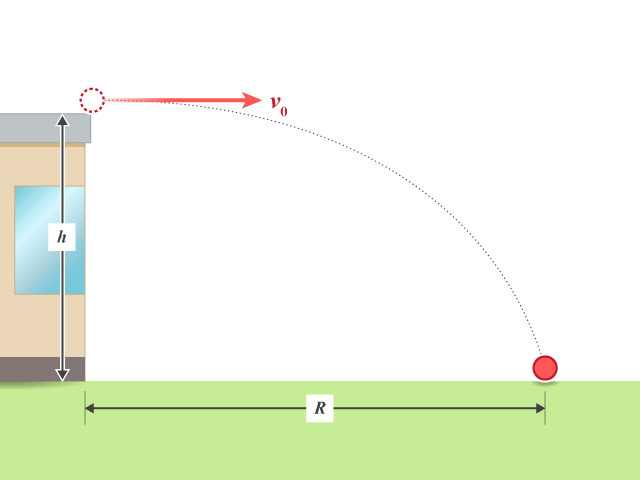
軌道 (trajectory) 用來描述拋體運動的路徑。
設向上為正、\({{v}_{0}}\) 為初速度(沿水平方向),一個進行平拋運動的物體,其水平和垂直方向的位移分別是:
\({{s}_{x}}={{v}_{0}}t\) ---------- (1)
\(\displaystyle{{{s}_{y}}=-\frac{1}{2}g\ {{t}^{2}}}\) ---------- (2)
合併方程 (1) 和 (2) 以消去 \(t\),可以得到一條描述平拋體的軌道的方程(見):
\(\displaystyle{{{s}_{y}}=-\frac{1}{2}g{{\left( \frac{{{s}_{x}}}{{{v}_{0}}} \right)}^{2}}}\)
留意上式為一條拋物線方程。