若一個距離地面高度為 \(h\) 的物體被水平投擲。經驗告訴我們,物體會遵循一個彎曲的路徑並最終掉在地上。我們想知道的是,物體的射程有多遠、多久後會着地,以及路徑的確實形狀。
中,物體 \(\rm{A}\) 與物體 \(\rm{B}\) 分別被水平投擲和自由釋放。換言之,物體 \(\rm{A}\) 在垂直方向沒有初速度。考慮兩物體相當於模擬程式中的砲彈,我們可以模擬的運動,結果會如所示。
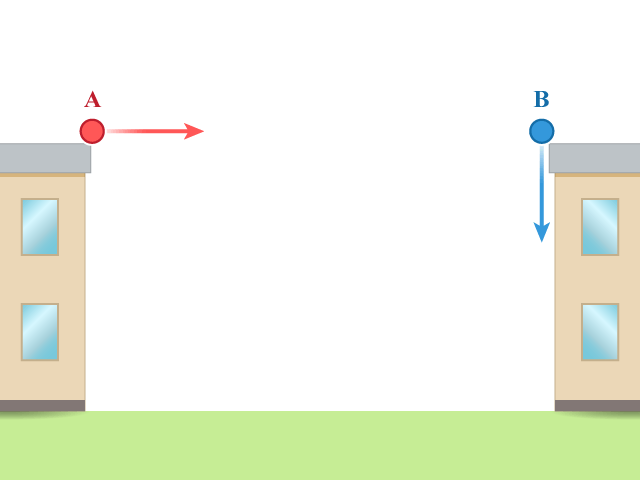
上方活動的結論為:分析運動時,物體的水平和垂直運動可以分開考慮。
設向上為正、\({{v}_{0}}\) 為物體的初速度(沿水平方向),一個平拋體在水平和垂直方向的速度和位移分別是
\({{v}_{x}}={{v}_{0}}\) \({{v}_{y}}=-g\ t\)
\({{s}_{x}}={{v}_{0}}t\) \(\displaystyle{{{s}_{y}}=-\frac{1}{2}g\ {{t}^{2}}}\)
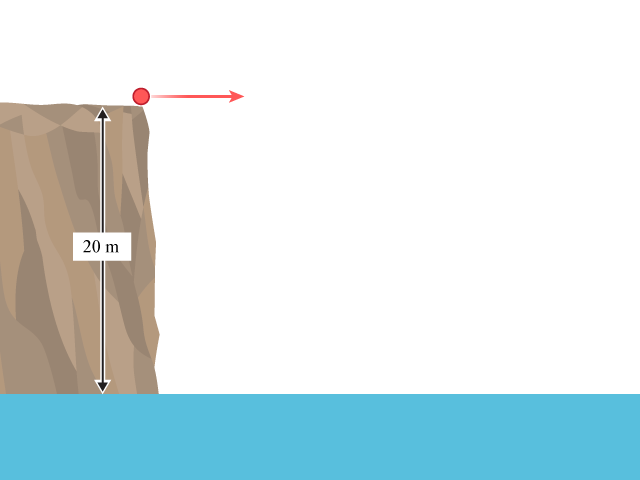
一個物體從 \(20 \text{ m}\) 高的懸崖被水平拋擲(),物體會經過多久後跌入海中?
【題解】
你可根據下方指示,先在模擬程式中設定的情境,演示物體的運動:
設物體起初位於原點,當位移的垂直分量等於 \(-20 \text{ m}\),物體跌入海中。應用勻加速運動方程:
\(\begin{align}{{s}_{y}} &= -\frac{1}{2}g\ {{t}^{2}} \\ -20\ \text{m} &= -\frac{1}{2}\left( 10\ \text{m}\ {{\text{s}}^{-2}} \right)\ {{t}^{2}} \\ t &= 2\ \text{s}\end{align}\)
留意我們不需要知道物體的初速度。