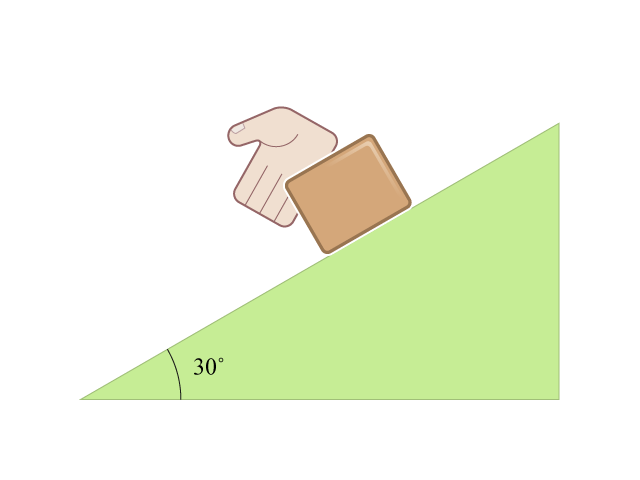
物體沿著斜面 (inclined plane) 作直線運動,也是牛頓運動定律一項重要的應用。如所示,一光滑斜面與水平成 \(30{}^\circ \),上有一個質量為 \(2 \text{ kg}\) 的方塊。方塊被釋放後,它的加速度為若干?
你可根據下方指示,先在《斜面模擬程式》中設定的情境,演示方塊的運動:
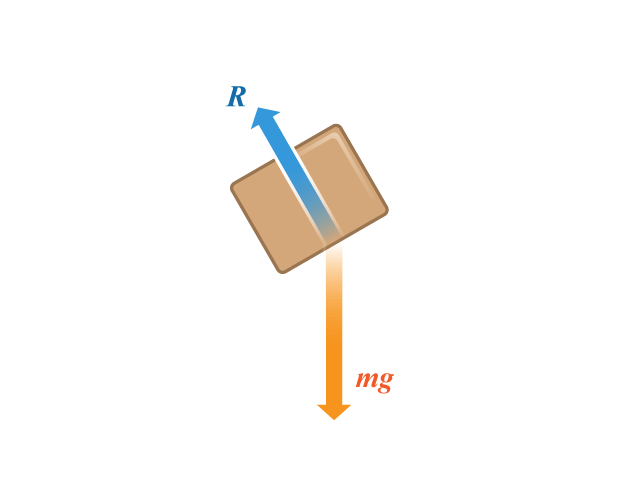
【步驟 \(1\)】:繪畫方塊的隔離體圖 解題思路
設 \(R\) 代表斜面對方塊的承托力。\(mg\) 是方塊的重量,如所示。
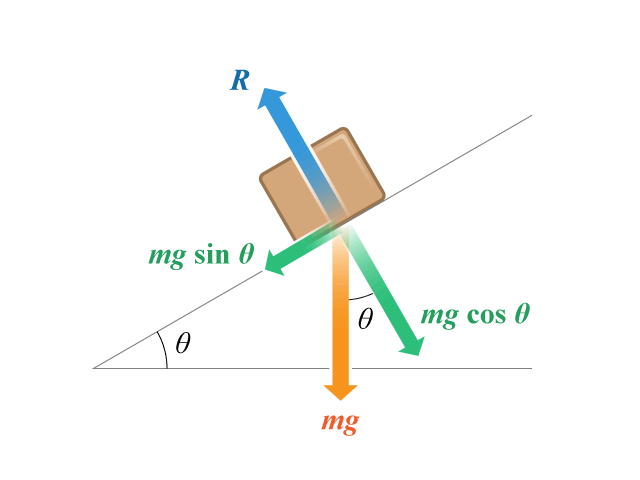
【步驟 \(2\)】:分解作用於方塊的力 解題思路
把所有作用於方塊上的力分解至兩互相垂直的方向(見):
【步驟 \(3\)】:計算方塊的加速度
在垂直於斜面的方向,方塊沒有加速度,淨力為零。根據牛頓第二定律:
\(\begin{align} R-mg\cos \theta &= 0 \\ \Rightarrow \ R &= mg\cos \theta \end{align}\)
這方程可用來計算承托力的大小。
在平行於斜面的方向,有一個 \(mg\sin \theta \) 的不平衡力。設加速度為 \(a\),根據牛頓第二定律:
\(mg\sin \theta =ma\) 注意點 \( \ \ \ \ \Rightarrow \ a=g\sin \theta \)
代入 \(\theta \) = \(30{}^\circ \) 和 \(g = 10 \text{ m}\ {{\text{s}}^{-2}}\),解方程後得 \(a = 5 \text{ m}\ {{\text{s}}^{-2}}\)。
上方的例子中,若斜面為粗糙,摩擦力會出現並阻礙方塊的運動。方塊被釋放後會否滑下,取決於摩擦力的大小。