你有留意到現實中有些情況,動量看來好像不守恆嗎?
一輛汽車撞上一道堅固的牆壁後,汽車便停下來。顯示:
【分析】若汽車與牆壁碰撞後均沒有動,碰撞後總動量便等於零(考慮汽車與牆壁為同一系統),這便違反了動量守恆定律?
其實,動量不是不守恆,而是我們察覺不到汽車減少了的動量到哪去。當汽車撞上一道牆壁後,牆壁便得到了汽車的動量。
因為牆壁是固定在地球上,所以地球在碰撞時也取得汽車的動量。但地球的質量是非常大,而所獲得的動量相對小很多,以致它的速度改變難以察覺。
我們會在下方定量分析表觀動量不守恆的例子。
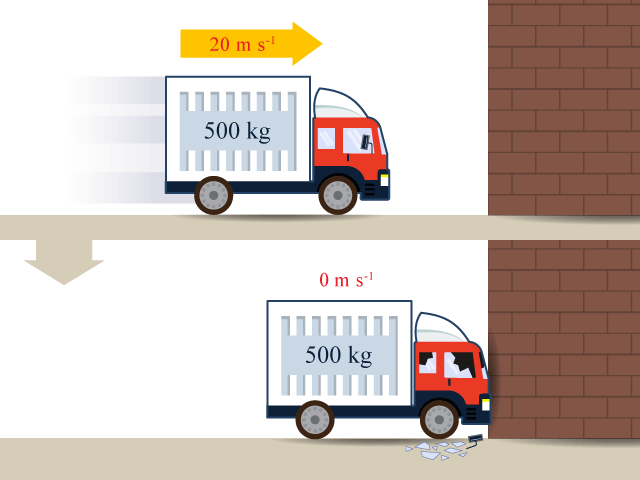
假設有一輛 500 \(\text{kg}\) 的貨車以 72 \(\text{km}\ {{\text{h}}^{-1}}\)(即 20 \(\text{m}\ {{\text{s}}^{-1}}\))撞擊一幅固定在地面的牆壁,然後在牆邊停下來()。在碰撞後牆壁並沒有損毀或倒下。地球(包括牆壁)的質量是 5.98 × 1024 \(\text{kg}\)。假設地球原本是靜止不動,我們可以計算碰撞後貨車和地球的速度。
【題解】設碰撞前的貨車運動方向為正、碰撞後貨車和地球的速度是 \(v\)。根據動量守恆定律:
碰撞前的總動量 \(=\) 碰撞後的總動量
\(\Rightarrow \left( 500\ \text{kg} \right)\left( \text{20 m}\ {{\text{s}}^{-1}} \right)+\left( 5.98\times {{10}^{24}}\ \text{kg} \right)\left( 0 \right)=\left( 500\ \text{kg}+5.98\times {{10}^{24}}\ \text{kg} \right)v\)
\(\Rightarrow v=1.67\times {{10}^{-21}}\ \text{m}\ {{\text{s}}^{-1}}\)
在碰撞後,貨車和地球的速度是 1.67 × 10−21 \(\text{m}\ {{\text{s}}^{-1}}\),這表示碰撞發生後,地球的速度只增加了 1.67 × 10−21 \(\text{m}\ {{\text{s}}^{-1}}\)。這個速度,約等於用 6 × 1018 \(\text{s}\),即 190 000 000 000 年的時間移動 1 \(\text{cm}\) 的距離,難怪我們難以察覺!