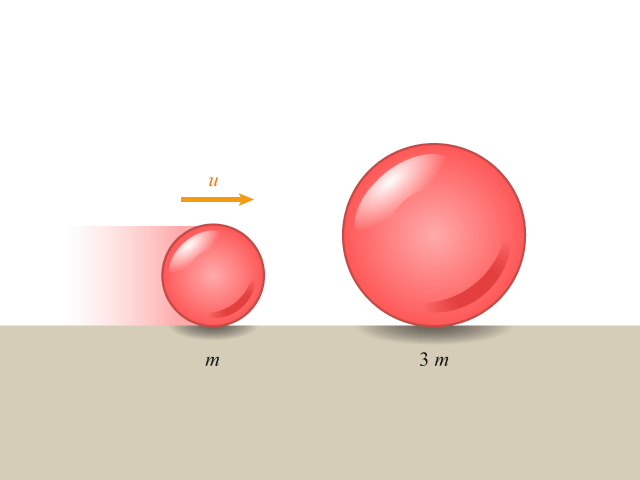
有一個質量爲 \(3m\) 的球靜止在平面上,另一個質量爲 \(m\) 的球以速度 \(u\) 撞向它。設質量爲 \(m\) 與質量為 \(3m\) 的球在碰撞後的速度分別為 \({{v}_{1}}\) 和 \({{v}_{2}}\)。
(a) 若碰撞為彈性碰撞,考慮兩球在碰撞前後的動能,試列出兩球碰撞後的速度與 \(u\) 之間的關係式。
【題解】 由於彈性碰撞的總動能守恆,可列出:
\(\displaystyle{\frac{1}{2}m\ {{u}^{2}}=\frac{1}{2}m\ {{v}_{1}}^{2}+\frac{1}{2}\left( 3m \right){{v}_{2}}^{2}}\)
\(\Rightarrow \ \ {{u}^{2}}={{v}_{1}}^{2}+3\ {{v}_{2}}^{2}\)
(b) 若兩球碰撞後黏在一起,試列出兩球碰撞後的速度與 \(u\) 之間的關係式。
【題解】 由於兩球碰撞後黏在一起,兩球的速度相同。設 \({{v}_{f}}\) 為碰撞後兩球的速度。根據動量守恆定律:
\(m\ u=\left( m+3m \right)\ {{v}_{f}}\)
\(\displaystyle{\Rightarrow \ \ {{v}_{f}}=\frac{u}{4}}\)