在上一課,我們已詳細討論以正弦公式來解三角形的所有邊長和角的大小。但正弦公式不能應用於所有類型的三角形,例如在圖右的兩個情境(第二個情境的應用在某些情形下比較繁複):
在本課,我們將探究以餘弦公式解這類的三角形。
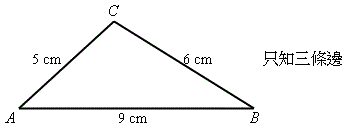
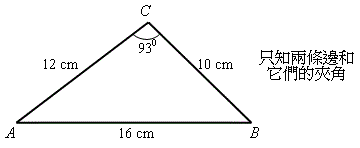
在未介紹餘弦公式前,我們首先做一個簡單的數學實驗。
在互動素材中,同學可以移動數值滑桿,輸入三角形的邊長\(\,a \)、\(\,b \,\)和\(\,c \,\)的數值。互動素材會根據這些數值繪畫三角形的圖像,並同時計算出這三角形的三隻角的正弦值。請觀察以下的三個比例的數值:
\(\, \displaystyle \alpha = \cos^{-1}{ (\frac{b^2+c^2-a^2}{2bc})}\)、\(\, \displaystyle \beta = \cos^{-1}{ (\frac{c^2+a^2-b^2}{2ca})}\)和
\(\, \displaystyle \gamma = \cos^{-1}{ (\frac{a^2+b^2-c^2}{2ab})}\)
根據圖中的資料完成下表。請限制角的範圍在\(\,0^\circ \,\)至\(\,180^\circ \,\)內,並如有需要,取角的答案準確至1\(\,^\circ \, \)及其他的答案準確至小數後兩個位。
|
\(\,a\) |
\(\,3\) |
\(\,4\) |
\(\,5\) |
\(\,4.5\) |
|
\(\,b\) |
\(\,4\) |
\(\,4\) |
\(\,5\) |
\(\,6\) |
|
\(\,c\) |
\(\,5\) |
\(\,4\) |
\(\,6\) |
\(\,2.5\) |
\(\,\frac{b^2+c^2-a^2}{2bc}\) |
\(\,0.8\) |
|||
|
\(\,\frac{c^2+a^2-b^2}{2ca}\) |
\(\,0.6\) |
\(\,0.5\) |
||
|
\(\,\frac{a^2+b^2-c^2}{2ab}\) |
\(\,0\) |
\(\,0.28\) |
||
\(\, \alpha = \cos^{-1} (\frac{b^2+c^2-a^2}{2bc})\) (\(\,\;^\circ\,\)) |
\(\,37\) |
\(\,43\) |
||
|
\(\, \beta = \cos^{-1} (\frac{c^2+a^2-b^2}{2ca})\) (\(\,\;^\circ\,\)) |
\(\,53\) |
|||
|
\(\, \gamma = \cos^{-1} (\frac{a^2+b^2-c^2}{2ab})\) (\(\,\;^\circ\,\)) |
\(\,90\) |
從以上的數學實驗,請回答以下關於在\(\,\triangle ABC\,\)中的 \(\, \displaystyle { \frac{b^2+c^2-a^2}{2bc}}\)、\(\, \displaystyle { \frac{c^2+a^2-b^2}{2ca}}\)和 \(\, \displaystyle { \frac{a^2+b^2-c^2}{2ab}}\):
| 1. | \(\,{\large \frac{b^2+c^2-a^2}{2bc} = \frac{c^2+a^2-b^2}{2ca} = \frac{a^2+b^2-c^2}{2ab}} \) | 是 否 |
| 2. | \(\,{\large \frac{b^2+c^2-a^2}{2bc} + \frac{c^2+a^2-b^2}{2ca} + \frac{a^2+b^2-c^2}{2ab}} = 1\) | 是 否 |
| 3. | \(\,\alpha = \beta = \gamma \) | 是 否 |
| 4. | \(\,\alpha + \beta + \gamma = 180^\circ\) | 是 否 |