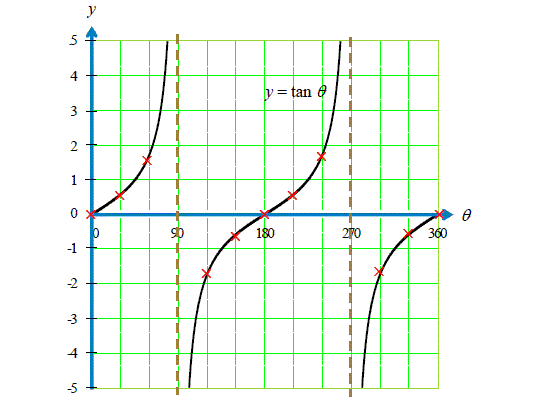
繪畫正切函數圖像,最傳統的方法是首先在下面的列表顯示一些\(\,\theta\,\)值和對應的\(\,y = tan \theta\,\)的值,其中\(\,0^\circ \le \theta \le 360^\circ\,\) 。如有需要,計算\(\,y \,\)值準確至二位小數。
| \(\theta \) | \({0^\circ}\) | \({30^\circ}\) | \({60^\circ}\) | \({90^\circ}\) | \({120^\circ}\) | \({150^\circ}\) | \({180^\circ}\) | \({210^\circ}\) | \({240^\circ}\) | \({270^\circ}\) | \({300^\circ}\) | \({330^\circ}\) | \({360^\circ}\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(y= \tan \theta \) | \( 0\) | \( 0.58\) | \( 1.73\) | --- | \( -1.73\) | \( -0.58\) | \( 0\) | \( 0.58\) | \( 1.73\) | --- | \( -1.73\) | \( -0.58\) | \( 0\) |
這列表也可以寫為
| \(\theta \) | \({0^\circ}\) | \({30^\circ}\) | \({60^\circ}\) | \({90^\circ}\) | \({120^\circ}\) | \({150^\circ}\) | \({180^\circ}\) | \({210^\circ}\) | \({240^\circ}\) | \({270^\circ}\) | \({300^\circ}\) | \({330^\circ}\) | \({360^\circ}\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(y= \tan \theta \) | \( 0\) | \( \frac{1}{{\sqrt 3 }}\) | \( {\sqrt 3 }\) | --- | \( -{\sqrt 3}\) | \( -\frac{1}{{\sqrt 3 }}\) | \( 0\) | \( \frac{1}{{\sqrt 3 }}\) | \( {\sqrt 3}\) | --- | \( -{\sqrt 3}\) | \( -\frac{1}{{\sqrt 3 }}\) | \( 0\) |
註:當\(\,\theta = 90^\circ\,\)及\(\,\theta = 270^\circ\),\(y = tan \theta\,\)的數值未能下定義。
根據在列表中的數值,我們可以畫出正切函數\(\,y = tan \theta\,\)的圖像,其中\(\,0^\circ \le \theta \le 360^\circ\,\) 。
請注意:當\(\,\theta = 90^\circ\,\)及\(\,\theta = 270^\circ\),\(y = tan \theta\,\)的圖像不是連續(discontinuous)的。
但這圖像是如何代表\(\,y = tan \theta\,\)?
你可以在互動素材中移動數值滑桿\(\,\theta\,\)的數值,並觀察\(\,\theta\,\)(以綠色代表) 及\(\,y\,\)(以紅色代表)的變化而得到的圖像。