對數的定義基於指數,實際生活中常用來模擬增長或衰減過程的指數函數,也可相應的轉化為對數函數。
依舊以指數函數的數學實驗中提及的三個例子為例,請回答相應的問題。
以下哪項函數能表示子細胞的個數 \(\displaystyle{ x }\) 與母細胞分裂次數 \(\displaystyle{ y }\) 的關係?
每種放射性元素經過半衰期後,其濃度降低至初始時的一半。現用碳十四 (\(C14\)) 測年法來測量生物標本的死亡時間,已知碳十四 (\(C14\)) 的半衰期是 \(\displaystyle{ t }\) 年,現有一生物標本,測得它的碳十四 (\(C14\)) 的含量將大約為生前的 \(\displaystyle{ x }\) 倍,則它的死亡年期 \(\displaystyle{ y }\) 是多少?
某人向銀行存入一筆 \(\displaystyle{ 10 }\) 萬元存款,年利率為 \(\displaystyle{ 2\% }\),利息的計算方式採用複利,新得到的利息同樣可以生息。該人計畫數年後從銀行取得 \(\displaystyle{ x }\) 萬元的本金加利息,則需要多長時間?
以上三個例子中的關係都屬於對數函數。
對數函數 (logarithmic function):設 \(\displaystyle{ a \gt 0 }\) 且 \(\displaystyle{a\ne 1 }\),則函數 \(\displaystyle{f\left( x \right)={{\log }_{a}}x }\) 稱為以 \(\displaystyle{ a }\) 為底的對數函數。
對數與指數的關係:若 \(\displaystyle{y={{a}^{x}} }\) ( \(\displaystyle{ a \gt 0 }\) 且 \(\displaystyle{a\ne 1 }\) ),則 \(\displaystyle{x={{\log }_{a}}y }\)。因此對數函數是指數函數的反函數,即若指數函數 \(\displaystyle{f\left( x \right)={{a}^{x}} }\),則其反函數為對數函數 \(\displaystyle{{{f}^{-1}}\left( x \right)={{\log }_{a}}x }\)。
對數函數和指數函數互為反函數,所以兩個函數都是表示自變量與應變量之間一對一的關係,既能通過垂直線測試法,又能通過水平線測試法。
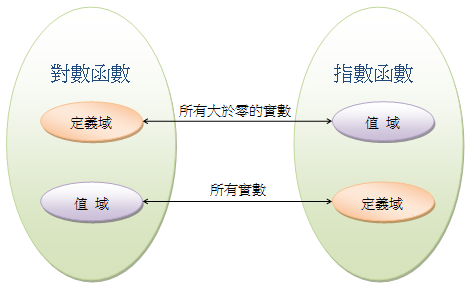
根據反函數的性質可知對數函數的定義域和值域,如圖所示。
當 \(\displaystyle{x \lt 0 }\) 時,\(\displaystyle{f\left( x \right)={{\log }_{a}}x }\) ( \(\displaystyle{ a \gt 0 }\) 且 \(\displaystyle{a\ne 1 }\)) 是不存在的。