下四分位數、中位數、上四分位數、最大值與最小值合稱五數綜合(five-number summary),這五個數字對一組數據提供了很重要的資料。我們可利用框線圖(box-and-whisker diagram,又稱箱形圖)來把這些資料以圖像表示出來。下圖顯示一框線圖及五個數字在圖中的位置。
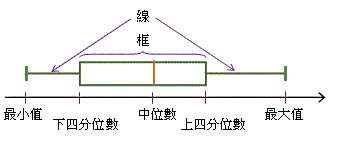
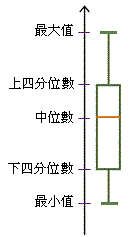
每兩個四分位數之間均包含\(\;25\%\;\)的數據,換言之,框線圖的框左和框右均包含\(\;25\%\;\)的數據,而中位數亦把框內的數據分成兩個\(\;25\%\;\)的部分。
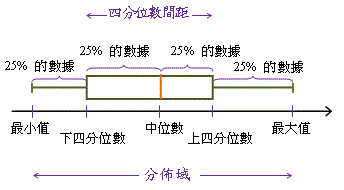
除了最大值、最小值和各個四分位數外,框線圖亦能準確表示一組數據的分佈域和四分位數間距(如附圖所示)。
提示
對於這組數據\(\;S\),我們有 \begin{align*} \hbox{最小值} &= 61 \\ \hbox{最大值} &= 78 \\ \hbox{中位數} &= \frac{1}{2}(65 + 69) = 67 \\ \hbox{下四分位數} &= 65 \\ \hbox{上四分位數} &= 73 \end{align*} 因此,這組數據的框線圖為
| 組區 | 頻數 |
|---|---|
| \(10-19\) | \(4\) |
| \(20-29\) | \(5\) |
| \(30-39\) | \(10\) |
| \(40-49\) | \(7\) |
| \(50-59\) | \(4\) |
提示
要找出這組數據的最大值、最小值及四分位數,我們可以繪畫這組數據的累積頻數多邊形。
從圖像可看到這組數據的資料: \begin{align*} \hbox{最小值} &= 9.5 \\ \hbox{最大值} &= 59.5 \\ \hbox{中位數} &= 35.5 \\ \hbox{下四分位數} &= 26.5 \\ \hbox{上四分位數} &= 44.5 \end{align*} 因此,這組數據的框線圖為
以下框線圖所示為\(\;28\;\)名學生在某次考試中的成績。
提示
以下框線圖所示為\(\;A\;\)學校和\(\;B\;\)學校在最近\(\;12\;\)場籃球比賽中的得分。