在初中時,我們學過弧的長度(弧長)與圓周之比和圓心角與周角 \(360^{\circ}\) 之比相同,即
\(\begin{align*} \displaystyle{\frac{弧長}{圓周}} &= \displaystyle{\frac{圓心角}{周角}} \ ,\\ \text{或可寫為 弧長:}\ 2\pi r &= \theta : 360 ^{\circ} \ ,\end{align*}\)
其中 \(r\) 是圓的半徑, \(\theta\) 是圓心角。
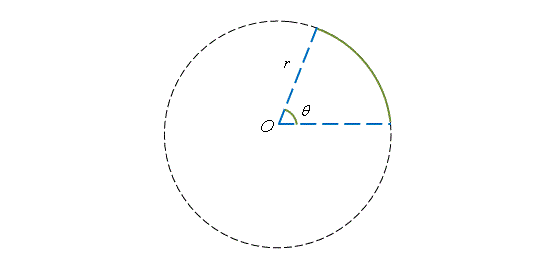
讓我們仔細地分析上述的結果。
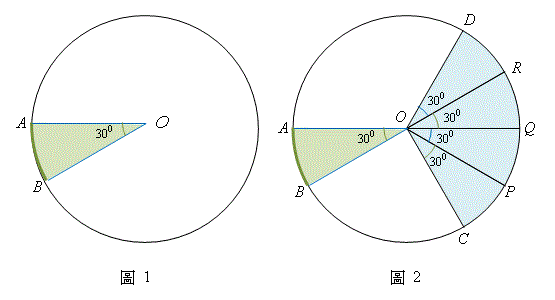
在圖 \(1\),\(OAB\) 是圓的扇形,而 \(\angle AOB = 30^{\circ}\)。現在將扇形 \(OAB\) 複製四次,並把它們並排而列。這可以形成一個圓心角為 \(120^{\circ}\) 的扇形 \(COD\) 之比相同(見圖 \(2\))。
從圖 \(1\) 及 \(2\),我們可以見到
\(\begin{align*} \overset{\frown}{AB} : \overset{\frown}{CD} &= 1 : 4 \\ \text{及} {\kern 20pt} \angle AOB : \angle COD &= 1 : 4 \ 。\end{align*}\)
結合以上兩個結果,我們可得
\(\overset{\frown}{AB} : \overset{\frown}{CD} = \angle AOB : \angle COD \;。\)
|
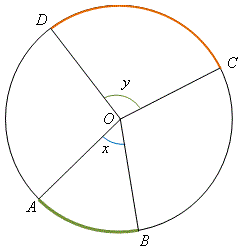
定理 \(16\)——弧與圓心角成比例 在一個圓中,弧的長度與所對的圓心角的大小成比例。 即是說,\(\overset{\frown}{AB} : \overset{\frown}{CD} = x : y \;。\) |
|
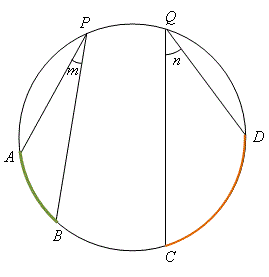
因為弧所對的圓心角兩倍於其圓周角,我們可以伸延「定理 \(10\)」 至以下:
|
定理 \(17\)——弧與圓周角成比例 在一個圓中,弧的長度與所對的圓周角的大小成比例。 即是說,\(\overset{\frown}{AB} : \overset{\frown}{CD} = m : n \;。\) |
|
定理 \(17\) 的証明: