從上一節的數學實驗中,我們探索到若兩個扇形的圓心角是相等,其相對的弧和弦都必定相等。
我們可利用以下六個定理來描述這屬性。
|
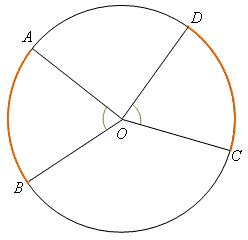
定理 \(10\)——等角對等弧 在一個圓中,相等的圓心角所對的弧均相等。 \(\begin{align*} \text{即是說,若} {\kern 10pt} \angle AOB &= \angle COD \ ,\\ \text{則} {\kern 57pt} \overset{\frown}{AB} &= \overset{\frown}{CD} \ 。\end{align*}\) |
|
|
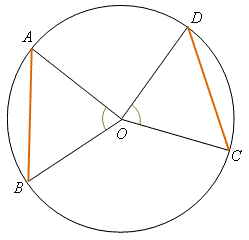
定理 \(11\)——等角對等弦 在一個圓中,相等的圓心角所對的弦均相等。 \(\begin{align*} \text{即是說,若} {\kern 10pt} \angle AOB &= \angle COD \ ,\\ \text{則} {\kern 57pt} {AB} &= {CD} \ 。\end{align*}\) |
|
以下是定理 \(10\) 和定理 \(11\) 的逆定理。
這是定理 \(10\) 的逆定理。
|
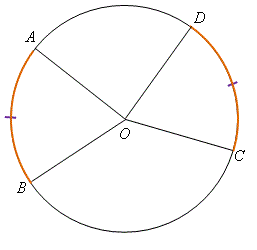
定理 \(12\)——等角對等弧 在一個圓中,相等的弧所對的圓心角均相等。 \(\begin{align*} \text{即是說,若} {\kern 18pt} \overset{\frown}{AB} &= \overset{\frown}{CD} \ ,\\ \text{則} {\kern 35pt} \angle AOB &= \angle COD \ 。\end{align*}\) |
|
這是定理 \(11\) 的逆定理。
|
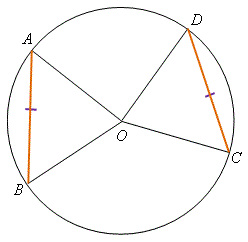
定理 \(13\)——等角對等弦 在一個圓中,相等的弦所對的圓心角均相等。 \(\begin{align*} \text{即是說,若} {\kern 18pt} {AB} &= {CD} \ ,\\ \text{則} {\kern 35pt} \angle AOB &= \angle COD \ 。\end{align*}\) |
|
根據定理 \(10\) 和定理 \(11\),我們可得以下兩個定理。
|
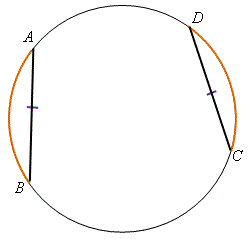
定理 \(14\)——等弦對等弧 在一個圓中,相等的弦所截得的弧均相等。 \(\begin{align*} \text{即是說,若} {\kern 18pt} {AB} &= {CD} \ ,\\ \text{則} {\kern 50pt} \overset{\frown}{AB} &= \overset{\frown}{CD} \ 。\end{align*}\) |
|
這是定理 \(14\) 的逆定理。
|
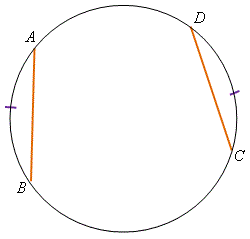
定理 \(15\)——等弧對等弦 在一個圓中,相等的弧所截得的弦均相等。 \(\begin{align*} \text{即是說,若} {\kern 18pt} \overset{\frown}{AB} &= \overset{\frown}{CD} \ ,\\ \text{則} {\kern 50pt} {AB} &= {CD} \ 。\end{align*}\) |
|