在右圖,\(AB\) 垂直於 \(OM\)。弦 \(AB\) 與圓心 \(O\) 之間的距離是垂線 \(OM\) 的長度。
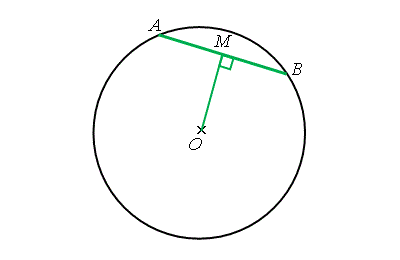
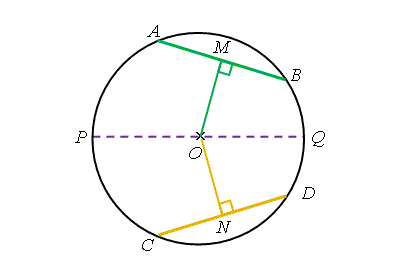
現在,把弦 \(AB\) 沿圓的直徑 \(PQ\) 反射可得到另外一條弦 \(CD\),而 \(CD\) 垂直離於 \(ON\)。根據對稱的原理, \(AB = CD\) 及 \(OM = ON\)。這顯示弦及它們與圓心之間的距離有一定的關係。
|
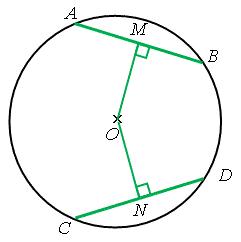
定理 \(4\) —— 等弦與圓心等距 兩條長度相等的弦必定與圓心等距。 即是說, |
|
定理 \(4\) 的証明:
從定理 \(4\),我們可以得到以下的逆定理。
|
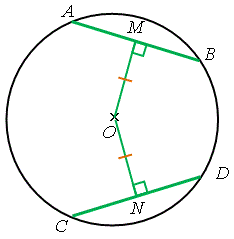
定理 \(5\) (定理 \(4\) 的逆定理) —— 與圓心等距的弦等長 兩條與圓心等距的弦的長度必定相等。 即是說, |
|