|
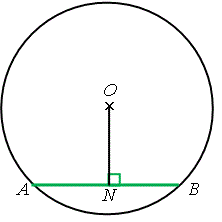
定理 \(1\) —— 圓心至弦的垂直線平分弦 由圓心至弦的垂線必定平分該弦。 即是說,若 \(ON \perp AB\), |
|
|
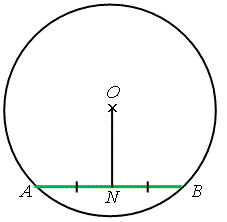
定理 \(2\) —— 圓心至弦中點的連線垂直弦 這是定理 \(1\) 的逆定理 連接由圓心至弦的中點的直線必定垂直於該弦。 即是說,若 \(AN = BN\), |
|
從定理 \(1\) 和定理 \(2\) 的結果,我們可以得到 \(ON\) 是弦 \(AB\) 的垂直平分線。由此,我們可以作出以下的推論:
|
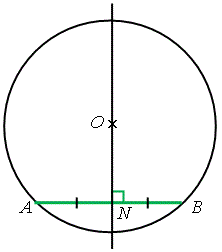
定理 \(3\) 一條弦的垂直平分線必定通過圓心。 |
|