用分數表示值循環小數 \(0.\dot{5}\)。
\(0.\dot{5} = 0.5555\dotso\)
\(= 0.5 + 0.05 + 0.005 + 0.0005 + \dotso\)
這數式其實是一個以首項 \(0.5\) 及公比為 \({\displaystyle{\frac{第 2 項}{首項}}} = {\displaystyle{\frac{1}{10}}}\) 的等比數項的無限項之和。
\(\therefore\)\(0.\dot{5} = {\displaystyle{\frac{0.5}{1 - \frac{1}{10}}}} = {\displaystyle{\frac{5}{9}}}\)
\(\therefore\)\(0.\dot{5} = {\displaystyle{\frac{5}{9}}}\)
用分數表示值循環小數 \(0.\dot3\dot{5}\)。
考慮等比數列 \(b^2, 2b, b + 1, \dotso\),其中 \(b \ne 0\)。
請在空位中填上適當的答案。
重温等比數列的性質:
若 \(T_1, T_2, T_3\) 是一個等比數列的三個連續項,則 \(T_1, T_2 \; 和 \; T_3\) 的關係可以用下列哪一項來表達?
| \(1.\) | \((T_1)(T_2) = (T_3)^2\) | \((首項) \times (第二項) = (第三項)^2\)。 |
| \(2.\) | \((T_2)(T_3) = (T_1)^2\) | \((第二項) \times (第三項) = (首項)^2\)。 |
| \(3.\) | \((T_1)(T_3) = (T_2)^2\) | \((首項) \times (第三項) = (第二項)^2\)。 |
\(T_1, T_2 \; 和 \; T_3\) 的關係是
\((T_1)(T_3) = (T_2)^2\)。
從已知的等比數列中,
\(\begin{align*}(b^2)(b + 1) &= (2b)^2 \\ b^2(b + 1) &= 4b^2 \\ b^2(b - 3) &= 0 \\ \therefore {\kern 40pt} b &= 3 {\kern 10pt} (\text{已知} \ b \ne 0 )\end{align*}\)
從 a,得知 \(b = 3\):
\(\begin{align*} \text{首項} & \ \ T_1 = b^2 = 9 \\ \text{第} 2 \text{項} & \ \ T_2 = 2b = 6 \\ \text{第} 3 \text{項} & \ \ T_3 = b + 1 = 4\end{align*}\)
\(\therefore\)公比 \(r = \displaystyle{\frac{2}{3}}\)
\(\therefore\)無限項之和
\(\begin{align*}S &= \frac{a}{1 - r} \\ &= \frac{9}{1 - \frac{2}{3}} \\ &= 27\end{align*}\)
在 \(2010\) 年,某城市有 \(12 000\) 名嬰兒出生。估計該城市的嬰兒出生人數每年以固定的百分數 \(a\%\) 增長。
請在空位中填上適當的答案。
從題目中, \(2010\) 年的嬰兒出生人數 \(= 12 000\)
\(\begin{align*}\therefore \quad & 2011 \ \text{年的嬰兒出生人數} \\ &= 12000(1 + a\%) \\ &= 1200(1+\frac{a}{100})\end{align*}\)
\(2010\) 年後的第 \(m\) 年的嬰兒出生人數
\(\begin{align*} &= 12000(1 + a\%)^m \\ &= 12000(1+\frac{a}{100})^m\end{align*}\)
請在右邊的圖中的空位中填上適當的答案。
從題目中得知嬰兒出生人數每年以 \(2\%\) 增長。
\(\therefore\)該等比數列的公比 \(= 1.02\)。
若以 \(S_n\) 表示等比數列首 \(n\) 項之和,則
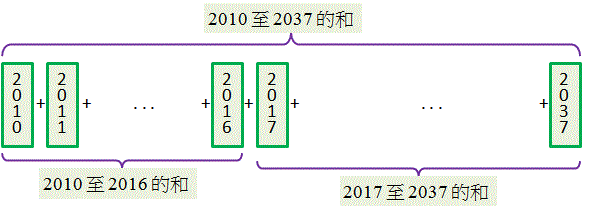
由 \(2017\) 年起至 \(2037\) 年出生嬰兒 \(= S_{28} – S_7\)
\(S_n = \displaystyle{\frac{a(r^n - 1)}{r - 1}}\)\(\begin{align*}S_{28} &= {\displaystyle{\frac{12000(1.02^{28} - 1)}{1.02 - 1}}} \\ &= 445000 \ (\text{準確至最接近的 } 1000)\end{align*}\)
\(\begin{align*}S_7 &= {\displaystyle{\frac{12000(1.02^7 - 1)}{1.02 - 1}}} \\ &= 89000 \ (\text{準確至最接近的 } 1000)\end{align*}\)
\(\begin{align*} S_7 - S_{28} &= 44500 - 89000 \\ &= 356000\end{align*}\)
\(\therefore\)由 \(2017\) 年起至 \(2037\) 年出生嬰兒共有 \(356 000\)(準確至最接近的 \(1000\))。
若以 \(2010\) 年嬰兒出生人數為等比數列的第 \(1\) 項,請填上以下不同年度的項數
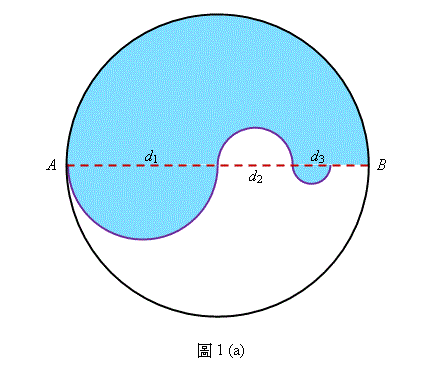
圖中所示為一個圓,其直徑 \(AB\) 長 \(64\) \(\text{cm}\)。在這個圓內有無限個直徑分別為 \(d_1, d_2, d_3, \dotso \) 的半圓,其中 \(AB = 2d_1 = 4d_2 = 8d_3 = \dotso \)。
請在空位中填上適當的答案。
已知 \(AB = 64\) \(\text{cm}\) 及 \(d_1\) 為半圓的半徑。
\(\therefore \quad\) \(d_1 = \) \(\text{cm}\)
利用相同的原因,
\(d_2 = \) \(\text{cm}\)
\(d_3 = \) \(\text{cm}\)
\(\dotso\)\(\dotso\)
我們可以看到 \(d_1, d_2, d_3, \dotso\) 組成一個等差數列。
該等比數列的首項 \(a\) 是 \(32\),而等比 \(r\)是 \(\displaystyle{\frac{1}{2}}\)。
\(\therefore \quad d_7 = ar^{n - 1} = 32({\displaystyle{\frac{1}{2}}})^6 = \displaystyle{\frac{1}{2}}\) \(\text{cm}\)。
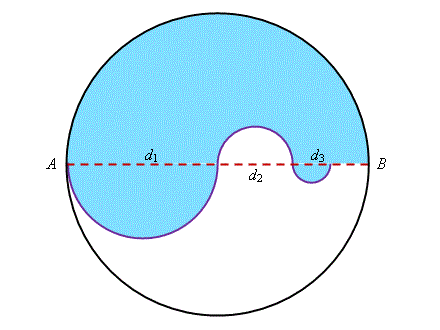
右邊的動畫可描述色部分的面積的形成。
區域 I:\(AB = 64\) \(\text{cm}\)
區域 I 的面積 \(=\) 直徑為 \(AB\) 的半圓的面積
\(= {\displaystyle{\frac{1}{2}}}\pi (32)^2\) \(\text{cm}\)\(^2\)
\(= 512\pi \) \(\text{cm}\)\(^2\)
區域 II:\(d_1 = 32\) \(\text{cm}\)
區域 II 的面積 \(=\) 直徑為 \(d_1\) 的半圓的面積
\(= {\displaystyle{\frac{1}{2}}}\pi (16)^2\) \(\text{cm}\)\(^2\)
\(= 128\pi \) \(\text{cm}\)\(^2\)
區域 III:\(d_2 = 16\) \(\text{cm}\)
區域 III 的面積 \(=\) 直徑為 \(d_2\) 的半圓的面積
\(= {\displaystyle{\frac{1}{2}}}\pi (8)^2\) \(\text{cm}\)\(^2\)
\(= 32\pi \) \(\text{cm}\)\(^2\)
區域 IV:\(d_3 = 8\) \(\text{cm}\)
區域 III 的面積 \(=\) 直徑為 \(d_2\) 的半圓的面積
\(= {\displaystyle{\frac{1}{2}}}\pi (4)^2\) \(\text{cm}\)\(^2\)
\(= 8\pi\) \(\text{cm}\)\(^2\)
\(\dotso\)
\(\therefore\)着色部分的面積
\(\begin{align*} =& \text{區域 I 的面積} + \text{區域 II 的面積} - \text{區域 III 的面積} + \text{區域 IV 的面積} \\ & - \dotso \\ =& \{512 + [128 - 32 + 8 - \dotso]\}\pi \ \text{cm}^2 \end{align*}\)
我們可以看到 \(128 - 32 + 8 - \dotso\) 是一個等比數列無限項的和,其首項為 \(128\), 公比為 \({\displaystyle{\frac{-32}{128}}} = -{\displaystyle{\frac{1}{4}}}\)。
此等比數列無限項的和為
\({\displaystyle{\frac{a}{1 - r}}} = -{\displaystyle{\frac{128}{1 - (-\frac{1}{4})}}} = 102.4\) (其中 \(r \lt 1\))
\(\therefore\)着色部分的面積 = \((512 + 102.4)\pi\) \(\text{cm}\)\(^2\ = 614.4 \pi\) \(\text{cm}\)\(^2\)。