我們在日常生活或者工程項目中經常需要計算一些物體的面積或者體積,這類問題都是幾何問題。在這一小節中,我們就來看一看二次方程在幾何問題上的應用吧。
如圖,公園中有一個長方形的魚池。為了方便遊客觀賞金魚,公園管理處決定在魚池周圍修建一條石子路。已知魚池的長為 \(10 \text{ m}\),闊 \(5 \text{ m}\)。管理處要求工程師修建石子路時保持它闊度均等並且總面積為 \(64 \text{ m}^2\),你能幫助工程師計算出石子路的闊度嗎?(準確至二位小數)
根據上小節,解決問題的步驟為
仔細閱讀並理解問題。
從題目中,我們知道這問題實際上是一條幾何題。已知的量包括小長方形(魚池)的長、闊,大長方形(石子路圍出來的長方形)與小長方形之間的面積。需要求出石子路的闊度。
根據題意,確定需要求解的未知數。
一般情況下,我們用 \(x\) 表示未知數。
我們需要尋找是石子路的闊度,所以可將這個未知量設為 \(x\) m。我們可以進一步把這個未知數在圖中標示出來。\(\qquad\)
根據題意,建立合適的方程。
我們須尋找等量的關係。在這題中,利用已知條件可以得到小長方形的面積,利用 \(x\) 可以得到大長方形的面積,而二者之差也是已知的,即石子路的面積。這樣,我們可以建立一個方程。
小長方形的面積 \(= 長 \times\ 闊 = 10 \times 5\)
大長方形的面積 \(= 長 \times\ 闊 = (10 + 2x) \times (5 + 2x)\)
石子路的面積 \(= (10 + 2x) \times (5 + 2x) - (10 \times 5) = 64\)
\(\therefore \; 2x^2 + 15x - 32 = 0\)
使用學過的方法解方程。
將上一步所得的二次方程變成一般式 \(ax^2 + bx + c = 0\),然後運用之前學過的方法解方程。
從 \(\; (10 + 2x) \times (5 + 2x) - (10 \times 5) = 64\)
\(\therefore \; 2x^2 + 15x - 32 = 0\)
利用二次公式可得
\(x = \large{\frac{-15 \pm \sqrt{15^2 - 4(2)(-32)}}{2(2)}}\) \(= -9.23 \; 或 \; 1.73\)
檢驗所得的解是否合理,捨去不合理的解。
所謂不合理的解,就是不合適題意的解。試想一想,如果得到的 \(x\) 是一個小於 \(0\) 的值,是否符合題目的要求呢?
(提示:題目要求出的是石子路的闊度,闊度能是負數嗎?)
回答題目的問題。
\(\therefore \; \)石子路的闊度為 \(1.73 \text{ m}\)。

請打開右面的模擬模型,並移動數值滑桿來代表魚池的 \( {\text{長}} = 10 \text{ m}\),\({\text{闊}} = 5 \text{ m}\),\({\text{和石子路的面積}} = 64 \text{ m}^2\)。
根據你所輸入的值,請細心觀察在模擬模型下一半的圖像表示魚池和石子路的大小,及根據以上尺寸計算出來石子路的闊度 \(x \ m\)。
請仔細思考及回答以下的問題:
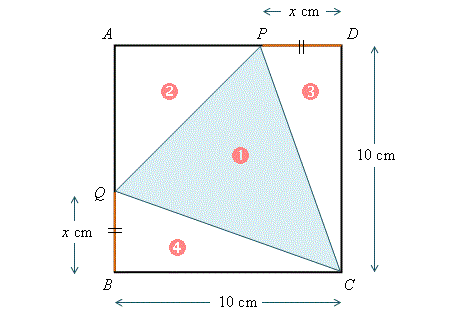
如圖,\(ABCD\) 是一個邊長為 \(10 \text{ cm}\) 的正方形,和 \(DP = BQ\)。已知 \(\triangle CPQ\) 的面積為 \(40 \text{ cm}^2\),求 \(DP\) 的長度(準確至二位小數)。
設 \(DP = x \text{ cm}\)。根據右圖,
\(\triangle CPQ\) 的面積
\( = ABCD\) 的面積 \(- \triangle APQ\) 的面積 \(- \triangle CDP\) 的面積 \(- \triangle BCQ \) 的面積
\(\begin{align*} \because \; \triangle CPQ \; \text{的面積} &= 40 \\ ABCD \; \text{的面積} &= 10^2 \\ \triangle APQ \; \text{的面積} &= \large{\frac{1}{2}} (10 - x)^2 \\ \triangle CDP \; \text{的面積} &= \large{\frac{1}{2}} (10) (x) \\ \triangle BCQ \; \text{的面積} &= \large{\frac{1}{2}} (10) (x) \end{align*}\)
\(\begin{align*} \therefore {\kern 52pt} 40 &= 10^2 - \large{\frac{1}{2}} (10 - x)^2 - \large{\frac{1}{2}} (10) (x) - \large{\frac{1}{2}} (10) (x) \\ 40 &= 100 - \large{\frac{1}{2}} (100 - 2x + x^2) - \large{\frac{1}{2}} 10x - \large{\frac{1}{2}} 10x \\ x^2 &= 20 \\ x &= 4.47 \ \text{或} \ -4.47 \end{align*}\)
\(\therefore \; DP\) 的長度為 \(4.47 \ \text{cm}\)。