孟德爾研究遺傳定律時,刻意集中觀察對比性狀。對比性狀的特點是有兩個極端,例如「高」與「矮」。為此,孟德爾在實驗前,先人工培育了有關的豌豆純種。
不過,在自然條件下,很多生物性狀跟豌豆高度的情況是不同的:在兩極之間呈連續分佈。
以香港男性的身高為例,\(18\;\)歲男性身高平均是\(\;172\; \rm{cm}\),標準差約\(\;5.6\; \rm{cm}\;\)的(\(2006\;\)年數據)——這代表我們身邊的\(\;18\;\)歲男性朋友中,\(95 \%\;\)的身高都在\(\;161\; \rm{cm}\;\)至\(\;183\; \rm{cm}\;\)之間;身高低於\(\;161\; \rm{cm}\;\)或高於\(\;183\; \rm{cm}\;\)的「極端」只佔少數。
進一步研究遺傳規律前,我們要先把性狀的變異區分。

幾個身高不同的男人
生物的變異分為兩種:
1. 不連續變異
性狀表徵 / 表達型能被明確分類,而且類別數量有限。
例子:豌豆是否皺摺、舌頭能否橫向捲曲、貓毛長短(自然狀態,見圖)、人類的\(\;\rm{ABO}\;\)血型系統等等。
不連續變異性狀不一定只有兩種表達型;可以肯定的是,表達型的分野明確,且數量有限。
不連續變異的例子:貓毛長度與人類血型
2. 連續變異
性狀表徵 / 表達型在兩個極端之間有許多中間類型,差異呈連續狀態,界限較不清楚;而且往往分佈數量在兩端很少,中間最多。
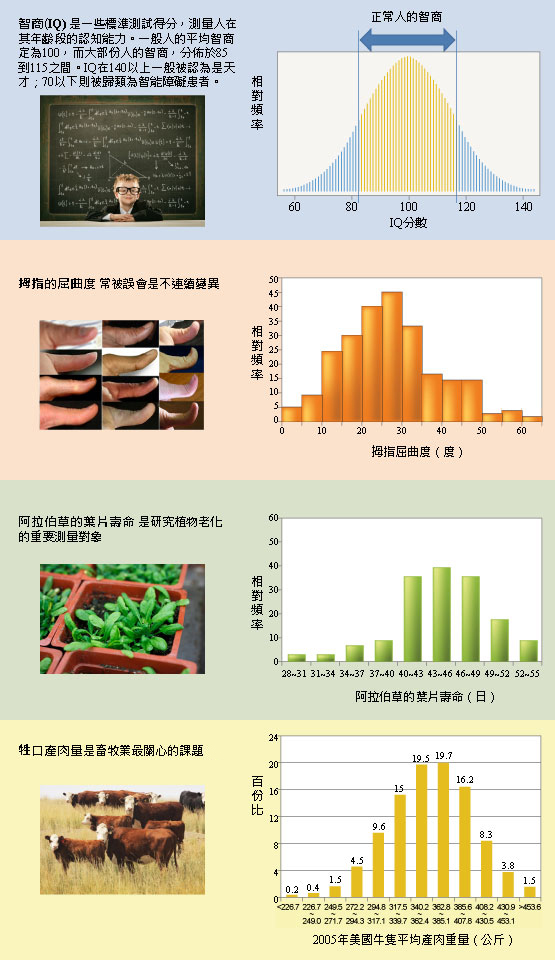
例子:身高、體重、智商、壽命。
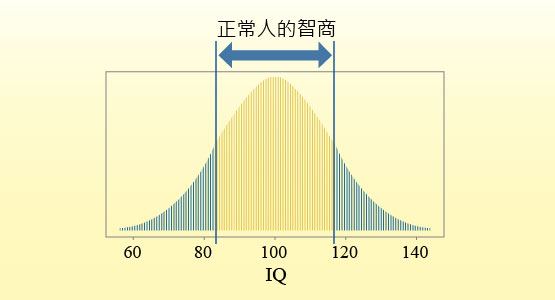
連續變異的例子:智商測驗結果分佈
不連續變異能明確地被分類,也能被量化,但其分佈不一定平均。
不連續變異的每種表達型,都可以有表達型以內的曲線分佈,全部個體不一定完全一樣,但不同的表達型之間一定有明確的分別。
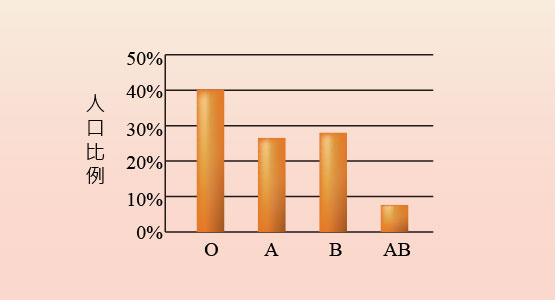
顯示香港人口中血型變異的條形圖
右圖以豌豆的高度為例子,我們來看看三代豌豆的高度變化是如何分佈的。
不連續變異的例子:三代豌豆的高度分佈
生物性狀通常牽涉很多基因,但只需要其中\(\;1\;\)個基因的變異,已足夠造成不連續變異。在這類變異中,基因座的等位基因種類數量與表達型的數量接近。
不連續變異的遺傳規律,可以用孟德爾定律分析。以下是一些例子:
| 不連續性狀 | 基因座 | 等位基因 | 基因型 | 表達型 |
|---|---|---|---|---|
 貓毛色素製造 |
White | W及w | WW | 沒有色素 (白色) |
| Ww | 沒有色素 (白色) | |||
| Ww | 有色素 (其它顏色) | |||
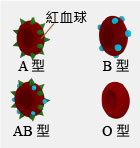 血型 |
I | IA, IB及IO | IAIA及IAIO | A型 |
| IBIB及IBIO | B型 | |||
| IOIO | O型 | |||
| IAIB | AB型 | |||
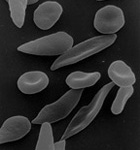 鐮形細胞貧血症 |
β-珠蛋白 | A及S | AA | 健康 |
| AS | 健康 | |||
| SS | 貧血 | |||
在連續變異中,性狀類別包括了從一個極端到另一個極端的許多中間類型,差異呈連續狀態。
連續變異的分佈,通常兩端的數量很少;越往中間,數量越多。用曲線表達,會得出一個 鐘形。這種分佈常見於各類統計,被稱為常態分佈曲綫。
顯示 110 名 7 歲男童身高變異分佈的直方圖
在生物界,連續變異性狀比不連續變異性狀更為普遍。以下是一些例子:
連續變異性狀的遺傳規律,跟不連續變異性狀很不一樣。簡單來說,有以下特點:
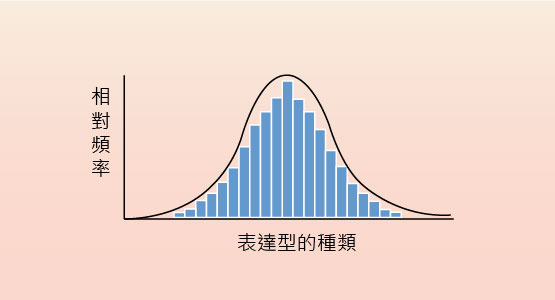
連續變異性狀可被視為很大數量的表達型