把牛頓萬有引力定律結合牛頓運動第二定律，便可以用來解釋行星圍繞太陽的運動，以及衛星圍繞地球的運動。

試考慮一顆行星以圓形路徑圍繞太陽運動（）。設軌道半徑為 \(r\)，行星與太陽之間，作用於行星上的萬有引力就是 \(F=G M m/{{r}^{2}}\)。這個力就提供了行星以勻速圓周運動時，所需的向心力，換言之：

\(\begin{align} & G\frac{M\ m}{{{r}^{2}}}=m\frac{{{v}^{2}}}{r} \\ & \Rightarrow v=\sqrt{\frac{G\ M}{r}} \\ \end{align}\)

上式就是行星在半徑為 \(r\) 的圓形軌道運動時的速率。從上方算式 \(v\)，我們也可推導出行星的軌道週期 \(T\) 等於：

\(\displaystyle{{{T}^{2}}=\frac{4{{\pi }^{2}}}{G\ M}{{r}^{3}}}\)                               推導方法

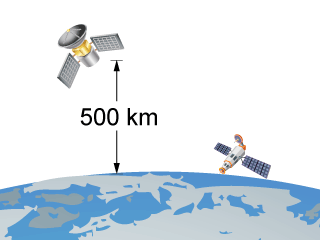
如所示，某人造衛星位於地球表面上方的 \(500 \;\text{km}\) 高度，另一個則貼近地球表面。試比較兩個人造衛星的速率。

【題解】

你可根據下方指示，先在模擬程式設定一個地球與人造衛星，演示人造衛星在引力下的圓周運動：

考慮位於地球表面上方 \(500 \;\text{km}\) 的人造衛星，其速率等於：

\(\begin{eqnarray} v &=& \sqrt{\frac{G\ M}{r}} \\ &=& \sqrt{\frac{\left( 6.67\times {{10}^{-11}}\ \text{N}\ {{\text{m}}^{2}}\text{k}{{\text{g}}^{-2}} \right)\left( \text{5}\text{.98}\times \text{1}{{\text{0}}^{\text{24}}}\ \text{kg} \right)}{6.38\times {{10}^{6}}\ \text{m}+500\ \text{m}}} \\ &=& 7.6\times {{10}^{3}}\ \text{m}\ {{\text{s}}^{-1}} \end{eqnarray}\)

若考慮位於接近地球表面的人造衛星，計算方法相同，但上式中 \(r\) 改為 \(6.38 × 10^{6} \;\text{m}\)，速率的計算結果等於 \(7.9 × 10^{3} \;\text{m}\ {{\text{s}}^{-1}}\)。