引力是任何兩個物體之間的一種吸引力。牛頓建議兩個質點之間的引力,可以用以下的方程計算():
\(\displaystyle{F=G\frac{{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}}\)
其中 \(G = 6.67 × 10^{-11}\; \text{N }{{\text{m}}^{2}}\text{ k}{{\text{g}}^{-2}}\),稱為引力常數 (gravitational constant)。\({{m}_{1}}\) 與 \({{m}_{2}}\) 是兩個質點的質量、\(r\) 代表兩個質點之間的距離。\(F\) 的方向平行於連接兩個質點之間的直線。
你可完成以下活動,進一步了解萬有引力定律:
補充資料:引力是甚麼?
重量就是星球與物體間的萬有引力,由此可知,物體在地球表面的重力加速度就是():
\(\displaystyle{g=\frac{G\ {{M}_{e}}}{{{R}_{e}}^{2}}}\)
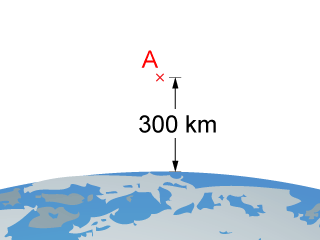
如所示,A 點位於地球表面上方 \(300 \;\text{km}\) 高度。試找出物體處於 A 點所具的重力加速度。
【題解】
你可根據下方指示,先在模擬程式中設定的情境,找出有關位置的重力加速度:
由於 A 點位於地球表面的上方,要計算該處物體的重力加速度,算式可以寫成:
\(\displaystyle{g \; =\frac{G\ {{M}_{e}}}{{{\left( {{R}_{e}}+h \right)}^{2}}}}\)
其中 \(h\) 是離地球表面的高度。由於地球的質量和半徑分別為 \(5.98 × 10^{24} \;\text{kg}\) 和 \(6.38 × 10^{6} \;\text{m}\),可知:
\(\begin{eqnarray} g &=& \frac{\left( 6.67\times {{10}^{-11}}\ \text{N}\ {{\text{m}}^{2}}\text{k}{{\text{g}}^{-2}} \right)\left( 5.98\times {{10}^{24}}\ \text{kg} \right)}{{{\left( 6.38\times {{10}^{6}}\ \text{m}+300\ \text{km} \right)}^{2}}} \\ &=& 8.94\ \text{m}\ {{\text{s}}^{-2}} \end{eqnarray}\)