[興倫智能課堂] 勻加速運動

勻加速運動模擬程式運動與線圖模擬程式

在學習勻加速運動之前，我們可先討論勻速運動。

甚麼是勻速運動 (uniform motion) 呢？勻速運動其實是勻加速運動的一個特例。

你可打開下方內容，根據指示先利用「運動與線圖模擬程式」演示運動，體驗勻速運動：

體驗勻速運動

試從模擬結果探究勻速運動的定義，在下方選擇正確的項目：

勻速運動是的運動。

【題解】
當物體進行勻速運動，它會以固定的速度運動，即是物體除了快慢不變（在相等的時間間距內行走相等距離）外，它的運動方向也不變。

換言之，下方動畫的蝴蝶雖然以固定速率飛行，但是飛行方向不斷改變，因此牠不是在做勻速運動。

當時間等於 \(0\) 與 \(t\) 時的位移分別是 \({{s}_{0}}\) 和 \(s\)，下方的關係式可用作計算 \(s\)：

\(s={{s}_{0}}+v\ t\)

試一試身手

蝴蝶以固定的速率及方向飛行，牠正在做勻速運動。

複數物體的運動

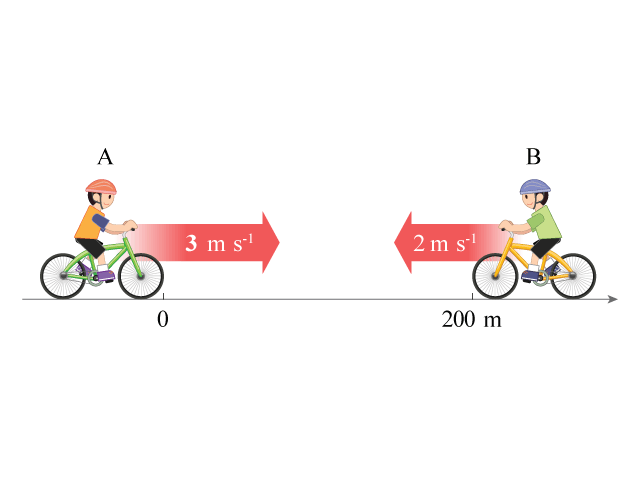
假設一輛自行車 \(\rm{A}\) 的起始位移是零，並以 \(3 \text{ m}\ {{\text{s}}^{-1}}\) 的速度行駛，如所示。同一時候，自行車 \(\rm{B}\) 從起始位移為 \(200 \text{ m}\) 的地方以 \(−2 \text{ m}\ {{\text{s}}^{-1}}\) 的速度運動。試計算時間經過多久後，兩輛自行車會相遇。

根據勻速運動關係式

\(s={{s}_{0}}+v\ t\)

分別考慮自行車 \(\rm{A}\) 與自行車 \(\rm{B}\) 的位移：

\({{s}_{\text{A}}}=0+3\ t=3\ t\)

\({{s}_{\text{B}}}=200+\left( -2 \right)\ t=200-2\ t\)

當兩輛自行車相遇時，它們的位移相同：

\(\begin{align}{{s}_{\text{A}}} &= {{s}_{\text{B}}} \\ 3\ t &= 200-2\ t \\ t &= 40\ \text{s}\end{align}\)

換言之，它們會於 \(40 \text{ s}\) 後於位移為 \(120 \text{ m}\) 處相遇。

試一試身手

多久後 \(\rm{A}\) 與 \(\rm{B}\) 會相遇？

在運動與線圖模擬程式選擇「\(1\text{D}\) 均速」、在線圖選「拖動：\(d_x\)」後，拖放藍色圓點繪出遞增的軌跡，如圖所示。

按「播放」後，程式演示一輛車子的勻速運動，留意車子的速度變化。

試更改線圖資料或其他設定，演示不同情況的車子運動，以鑑定勻速運動的要點。

我們可以根據速度的定義：

\(\displaystyle{v=\frac{\delta s}{\delta t}}\)

推導一條用作計算位移的關係式。

當時間等於 \(0\) 與 \(t\) 時的位移分別是 \({{s}_{0}}\) 和 \(s\)。在勻速運動中，上式可以寫成：

\(\displaystyle{v=\frac{\Delta s}{\Delta t}=\frac{s-{{s}_{0}}}{t-0}}\)

\(\Rightarrow s={{s}_{0}}+v\ t\)

【問題 \(1\)】
某物體含起始位移 \(−10 \text{ m}\)。它以 \(5 \text{ m}\ {{\text{s}}^{-1}}\) 的固定速度進行直線運動。甚麼時候物體會到達位移等於 \(10 \text{ m}\) 的位置？

【題解】
設到達位移為 \(10 \text{ m}\) 位置所費時間是 \(t\)。考慮：

\(s={{s}_{0}}+v\ t\)

\(\text{m}\) = \(\text{m}\) + ( \(\text{m}\ {{\text{s}}^{-1}}\)) \(t\)

\(t\) = \(\text{s}\)

【題解】
物體的速度為正，表示向位移增加的方向運動。根據勻速運動的關係式：

\(\begin{align}s &= {{s}_{0}}+v\ t \\ 10\ \text{m} &= -10\ \text{m}+\left( 5\ \text{m}\ {{\text{s}}^{-1}} \right)\ t \\ t &= 4\ \text{s}\end{align}\)

若在勻加速運動模擬程式設定 \(v = 5 \text{ m}\ {{\text{s}}^{-1}}\)、\(a = 0 \text{ m}\ {{\text{s}}^{-2}}\)，並把小球拖至 \(−10 \text{ m}\) 的位置後按播放，可觀察到小球位移為 \(10 \text{ m}\) 時，\(t = 4 \text{ s}\)。

【問題 \(2\)】
承上題，物體到達位移為 \(10 \text{ m}\) 的位置後，所行走的距離為若干？

A. \(0 \text{ m}\)

B. \(10 \text{ m}\)

C. \(20 \text{ m}\)

D. \(-10 \text{ m}\)

【題解】
如圖所示，由於物體的起始位移 \(= −10 \text{ m}\)、最終位移 \(= 10 \text{ m}\)，所以行走的距離 \(= 20 \text{ m}\)。

物體 \(\rm{A}\) 以 \(3 \text{ m}\ {{\text{s}}^{-1}}\) 的速度從 \(O\) 點出發。物體 \(\rm{B}\) 則於 \(4\) 秒後，在同一地點以 \(5 \text{ m}\ {{\text{s}}^{-1}}\) 的速度出發。物體 \(\rm{B}\) 需時多久才追上物體 \(\rm{A}\)？

A. \(5 \text{ s}\)

B. \(10 \text{ s}\)

C. \(12 \text{ s}\)

D. \(15 \text{ s}\)

【題解】
已知勻速運動關係式 \(s={{s}_{0}}+v\ t\)。

先考慮物體 \(\rm{B}\) 出發前，物體 \(\rm{A}\) 在 \(4\) 秒內的運動：

\({{s}_{\text{A}1}}=0+\left( 3\ \text{m}\ {{\text{s}}^{-1}} \right)\left( 4\ \text{s} \right)=12\ \text{m}\)

\({{s}_{\text{A}1}}\) 可想像為物體 \(\rm{B}\) 出發時，物體 \(\rm{A}\) 的起始位移。

設物體 \(\rm{B}\) 需 \(t\) 秒才追上物體 \(\rm{A}\)。換言之，即是物體 \(\rm{B}\) 出發後，需 (\(t\) − 4) 秒才追上物體 \(\rm{A}\)。考慮物體 \(\rm{B}\) 出發後，兩物體的位移：

\({{s}_{\text{A}2}}=12+3\left( t-4 \right)=3\ t\)

\({{s}_{\text{B}2}}=0+5\left( t-4 \right)=5\ \left( t-4 \right)\)

當物體 \(\rm{B}\) 追上物體 \(\rm{A}\) 時，它們的位移相同：

\(\begin{align}{{s}_{\text{A}2}} &= {{s}_{\text{B}2}} \\ 3\ t &= 5\ \left( t-4 \right) \\ t &= 10\ \text{s}\end{align}\)

你也可以使用「勻加速運動模擬程式」來驗證計算結果。