為要描述物體速度變化的快慢(速度並非固定的情況),運動學上定義了加速度 (acceleration)。
| 符號 | 定義 | 單位 | 標量/矢量? |
|---|---|---|---|
| \(a\) | 速度的變化率 \(\displaystyle{a=\frac{\text{速度變化}}{\text{變化所用時間}}}\) | \(\text{m}\ {{\text{s}}^{-2}}\) | 矢量 |
【例子】 某物體在 \(5\) 秒時間內,把速度從 \(2.0 \text{ m}\ {{\text{s}}^{-1}}\) 均勻地增加至 \(12.0 \text{ m}\ {{\text{s}}^{-1}}\),物體的加速度便是:
\(\begin{align}\text{物體加速度} &= \text{速度變化 / 變化所用時間} \\ &= \frac{12\ \text{m}\ {{\text{s}}^{-1}}-2\ \text{m}\ {{\text{s}}^{-1}}}{5\ \text{s}} \\ &= 2 \text{ m}\ {{\text{s}}^{-2}}\end{align}\)
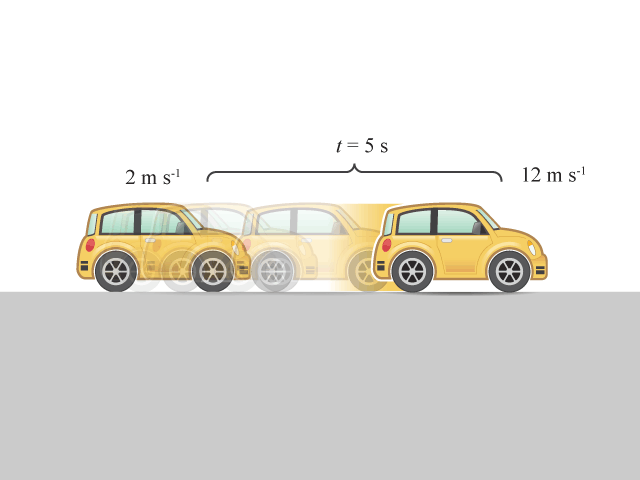
當物體從時間 \(t\) 至 \(t\) + \(\Delta t\) 的速度變化為 \(\Delta v\),可定義平均加速度:
平均加速度 \(\displaystyle{\bar{a}=\frac{\Delta v}{\Delta t}}\)
若考慮速度在一個很短的時間間距 (\(\delta t\)) 內出現了變化 \(\delta v\),則瞬時加速度定義為:
瞬時加速度 \(\displaystyle{a=\frac{\delta v}{\delta t}}\)
【例子】
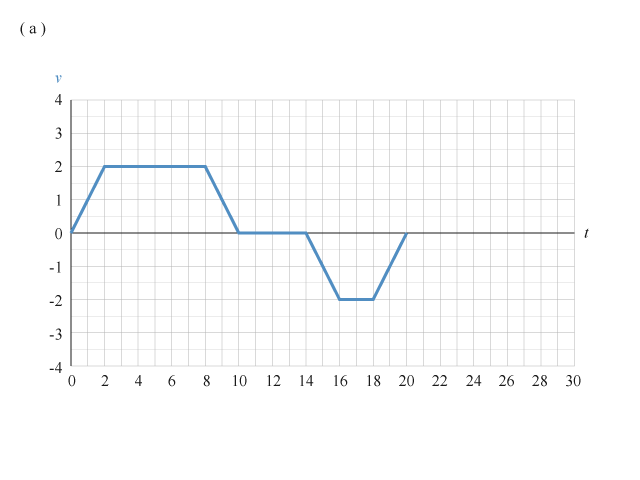
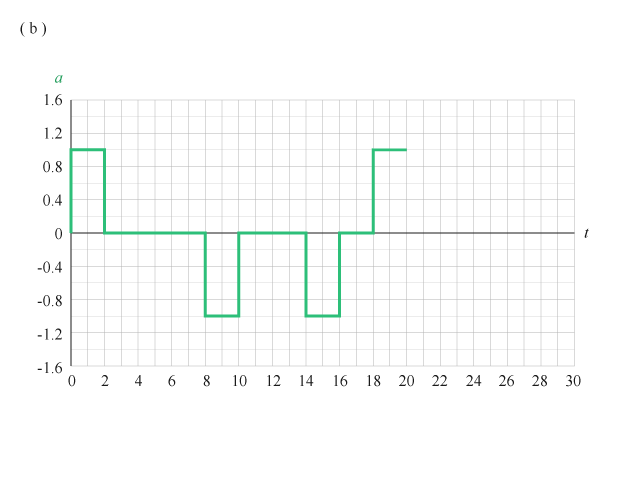
(a) 顯示某物體的速度隨時間變化,它在 \(20 \text{ s}\) 內的瞬時加速度就如(b) 所示。但物體的平均加速度,如考慮從 \(4 \text{ s}\) 至 \(16 \text{ s}\) 間,就是:
\(\begin{align}\bar{a} &= \frac{-2\ \text{m}\ {{\text{s}}^{-1}}-2\ \text{m}\ {{\text{s}}^{-1}}}{16\ \text{s}-4\ \text{s}} \\ &= -0.333 \text{ m}\ {{\text{s}}^{-2}}\end{align}\)
你也可以模仿(a),在運動與線圖模擬程式繪畫 \(v\)-\(t\) 線圖後,觀看 \(a\)-\(t\) 和 \(s\)-\(t\) 線圖,並演示物體的運動。(選「\(1\text{D}\) 均速」和「拖動:\(v_x\)」後,拖放藍色圓點可繪畫 \(v\)-\(t\) 線圖)
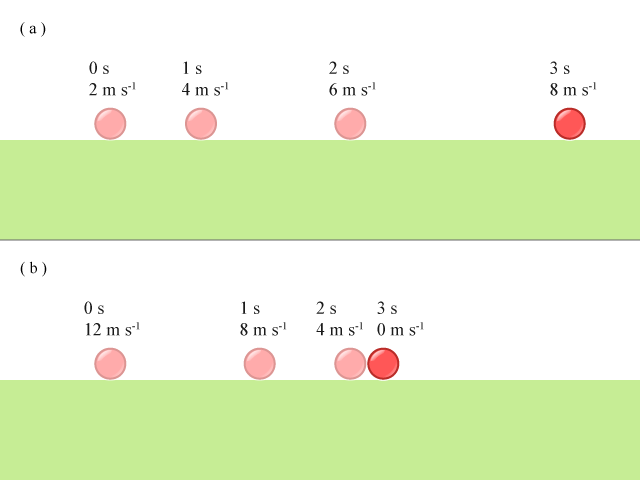
在直線運動中,加速度的正負能反映速度乃增加還是減少:
若加速度為正 (\(a\) > 0),代表速度增大;
若加速度為負 (\(a\) < 0),代表速度減小。
留意負的加速度有時會稱作減速度 (deceleration)。
【例子】
考慮一個小球有固定的加速度 \(a = 2 \text{ m}\ {{\text{s}}^{-2}}\)。當小球於 \(t = 0\) 的速度為 \(2 \text{ m}\ {{\text{s}}^{-1}}\)(即 \(t = 0\) 的速度,設符號為 \(u\)),隨後 \(3\) 秒的小球位置和速度便如(a) 所示,速度的量值增加。
若小球的加速度為負,如 \(a = -4 \text{ m}\ {{\text{s}}^{-2}}\),而起始的速度 \(u = 12 \text{ m}\ {{\text{s}}^{-1}}\) 的話,隨後 \(3\) 秒的小球位置和速度便如(b) 所示,速度的量值減少。
【根據,請於下方選擇正確的項目】 使用模擬程式
在(b) 的小球運動中,當 \(t = 6 \text{ s}\),小球的運動狀態如何?
(1)小球的位移變化等於 \(0\)
(2)小球的速度等於 \(0\)
(3)小球改變運動方向
【題解】 由於 \(a < 0\) 會令小球速度不斷減小,當 \(t = 3 \text{ s}\),小球的速度等於 \(0\),並改變運動方向,之後改為以負的速度運動。 當 \(t = 6 \text{ s}\),小球回到 \(t = 0\) 的位置,換言之,其位移變化等於 \(0\)。
【題解】 由於 \(a < 0\) 會令小球速度不斷減小,而 \(u < 0\),所以小球的速度會「愈來愈負」,換言之,小球速率則愈來愈大。