牛頓運動第二定律確定了運動和力的關係,公式:
\({{F}_{net}}=m\ a\)
把物體的運動與受力情況聯繫起來()。知道了物體的受力情況,便能確定物體的運動狀態如何改變了。
同學可以透過下面討論的例子,掌握運用牛頓運動第二定律去解決問題:
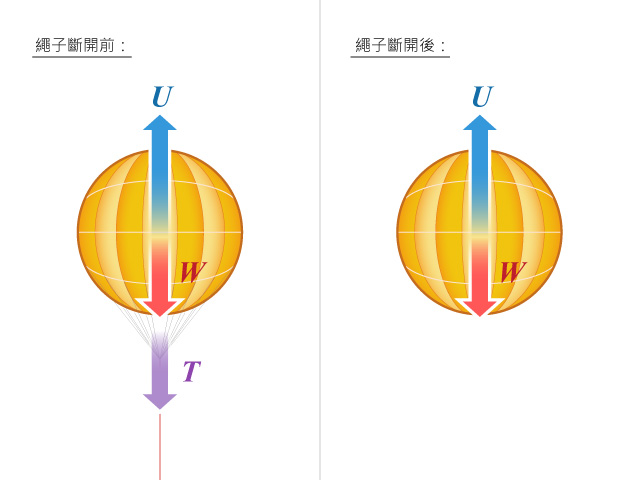
一個質量為 \(150 \text{ kg}\) 的熱汽球以輕繩綁在地上()。由於物體在空氣中會受到浮力的作用,若繩子斷開,汽球以 \(2 \text{ m}\ {{\text{s}}^{-2}}\) 的加速度上升。求繩子的張力。

【步驟 \(1\)】:繪畫汽球的隔離體圖 解題思路
設 \(W\)、\(U\) 和 \(T\) 分別代表重量、浮力和張力,如所示。
【步驟 \(2\)】:計算前,要設定正 (+) 的方向,可選向上為正方向。 解題思路
【步驟 \(3\)】:分析繩子斷開前的力 解題思路
起初,汽球綁在地上並保持靜止,作用於汽球上的淨力等於零。換言之,
\({{F}_{net}}=U-W-T=0\) 注意點 \(\Rightarrow \ \ T=U-W\)
【步驟 \(4\)】:分析繩子斷開後的力
繩子斷開後,作用於汽球上的淨力等於 \(U\) − \(W\)。根據牛頓第二定律:
\(\begin{align}{{F}_{net}} &= m\ a \\ U-W &= m\ a \\ &= \left( 150\ \text{kg} \right)\left( 2\ \text{m}\ {{\text{s}}^{-2}} \right) \\ &= 300\ \text{N}\end{align}\)
【步驟 \(5\)】:計算繩子的張力
合併步驟 \(3\) 和 \(4\) 的結果,得:
\(\begin{align}T &= U-W \\ &= 300\ \text{N}\end{align}\)
兩個質量分別為 \(5 \text{ kg}\) 與 \(3 \text{ kg}\) 的方塊以輕繩相連,靜止在一光滑的水平桌上()。若有一 \(10 \text{ N}\) 的水平力作用於方塊組的一端,求各方塊的加速度。
你可根據下方指示,先在《方塊列模擬程式》中參考的情境設定,演示方塊的運動:
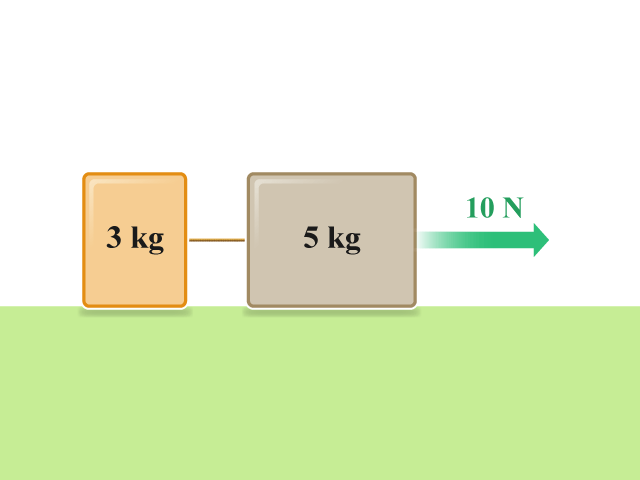
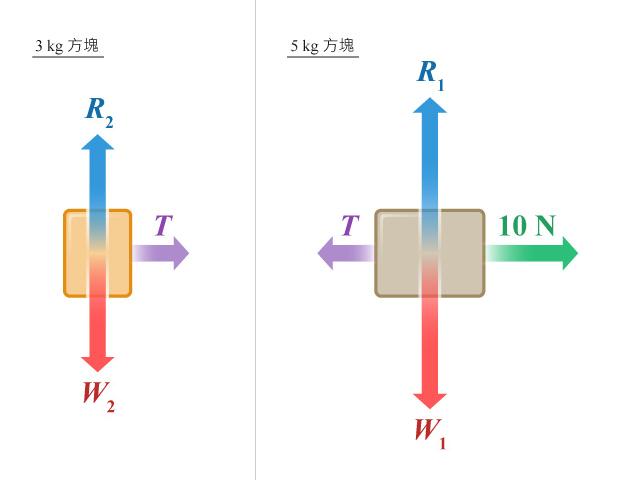
【步驟 \(1\)】:繪畫方塊的隔離體圖 解題思路
設 \(W\)、\(R\) 和 \(T\) 分別為重量、承托力和張力。「\(1\)」和「\(2\)」分別代表 \(5 \text{ kg}\) 方塊和 \(3 \text{ kg}\) 方塊,如所示。
【步驟 \(2\)】:分析作用於方塊的淨力 解題思路
作用於 \(3 \text{ kg}\) 方塊上的淨力:\({{F}_{net2}}=T\) 作用於 \(5 \text{ kg}\) 方塊上的淨力:\({{F}_{net1}}=10\ \text{N}-T\) 注意點
【步驟 \(3\)】:計算方塊的加速度
分別應用牛頓第二定律於 \(3 \text{ kg}\) 和 \(5 \text{ kg}\) 方塊:
\(T=\left( 3\ \text{kg} \right)\ a\) 注意點 \(10\ \text{N}-T=\left( 5\ \text{kg} \right)\ a\)
解方程後得 \(a = 1.25 \text{ m}\ {{\text{s}}^{-2}}\) 和 \(T = 3.75 \text{ N}\)。
作為參考,本題也有其他解題方法。就是考慮該兩個方塊作為一個 \(8 \text{ kg}\) 方塊。
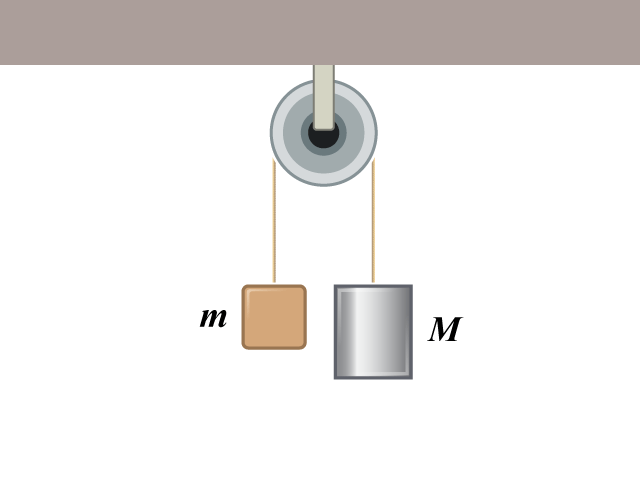
兩個質量分別為 \(m = 4.0 \text{ kg}\) 和 \(M = 6.0 \text{ kg}\) 的方塊以輕繩連接,並繞過一個滑輪()。兩方塊原本被握住並處於靜止狀態,然後突然釋放。求各方塊的加速度。
你可根據下方指示,先在《斜面模擬程式》中設定類似的情境,演示方塊的運動:
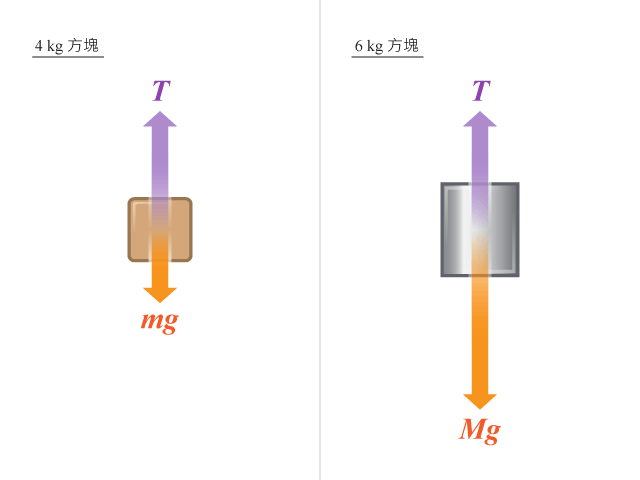
【步驟 \(1\)】:繪畫方塊的隔離體圖 解題思路
設 \(T\) 為張力、\(mg\) 與 \(Mg\) 分別代表 \(4 \text{ kg}\) 方塊和 \(6 \text{ kg}\) 方塊的重量,如所示。
【步驟 \(2\)】:根據牛頓定律列出關係式 解題思路
作用於 \(4 \text{ kg}\) 方塊:\(mg-T=m\left( -a \right)\) 作用於 \(6 \text{ kg}\) 方塊:\(Mg-T=M\ a\) 注意點
【步驟 \(3\)】:計算方塊的加速度
用步驟 \(2\) 內的兩道方程可解出 \(a\) 和 \(T\),結果為:
\(\displaystyle{a=\frac{M-m}{M+m}g}\) \(\displaystyle{T=\frac{2Mm}{M+m}g}\) 注意點
代入 \(m = 4 \text{ kg}\)、\(M = 6 \text{ kg}\) 和 \(g = 10 \text{ m}\ {{\text{s}}^{-2}}\),解方程後得 \(a = 2 \text{ m}\ {{\text{s}}^{-2}}\) 和 \(T = 48 \text{ N}\)。
作為參考,本題也有其他解題方法。就是考慮該兩個方塊作為一個 \(10 \text{ kg}\) 方塊。
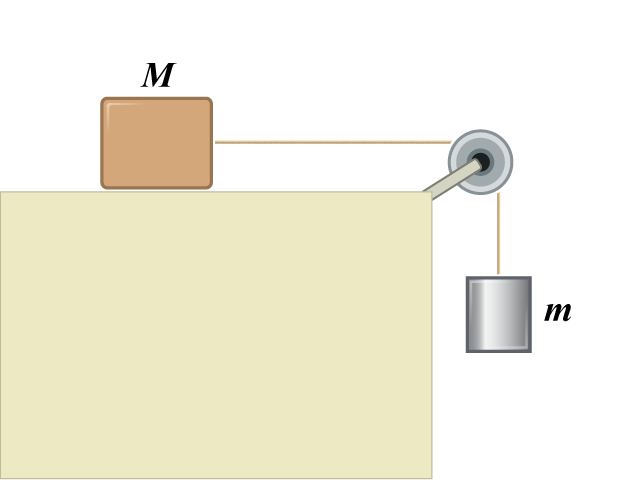
顯示,一個質量為 \(M = 8.0 \text{ kg}\) 的箱子以輕繩與質量為 \(m = 2.0 \text{ kg}\) 的砝碼連接 (\(m\) < \(M\)),並繞過一個滑輪。忽略摩擦力,求箱子與砝碼的加速度,以及繩子的張力。
你可根據下方指示,先在《斜面模擬程式》中設定類似的情境,演示箱子與砝碼的運動:
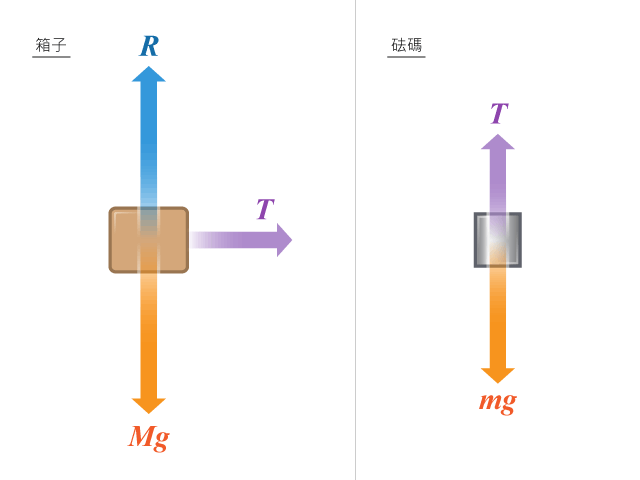
【步驟 \(1\)】:繪畫箱子與砝碼的隔離體圖 解題思路
設 \(T\) 為張力、\(R\) 為承托力、\(Mg\) 與 \(mg\) 分別是箱子和砝碼的重量,如所示。
【步驟 \(2\)】:根據牛頓定律列出關係式 解題思路
作用於 \(8 \text{ kg}\) 箱子:\(T=M\ a\) 作用於 \(2 \text{ kg}\) 砝碼:\(mg-T=m\ a\) 注意點
【步驟 \(3\)】:計算加速度與繩子的張力
用步驟 \(2\) 內的兩道方程可解出 \(a\) 和 \(T\),結果為:
\(\displaystyle{a=\frac{m}{m+M}g}\) \(\displaystyle{T=\frac{M}{m+M}mg}\) 注意點
代入 \(M = 8 \text{ kg}\)、\(m = 2 \text{ kg}\) 和 \(g = 10 \text{ m}\ {{\text{s}}^{-2}}\),解方程後得 \(a = 2 \text{ m}\ {{\text{s}}^{-2}}\) 和 \(T = 16 \text{ N}\)。
作為參考,本題也有其他解題方法。就是考慮箱子與砝碼為一個單一的物體。
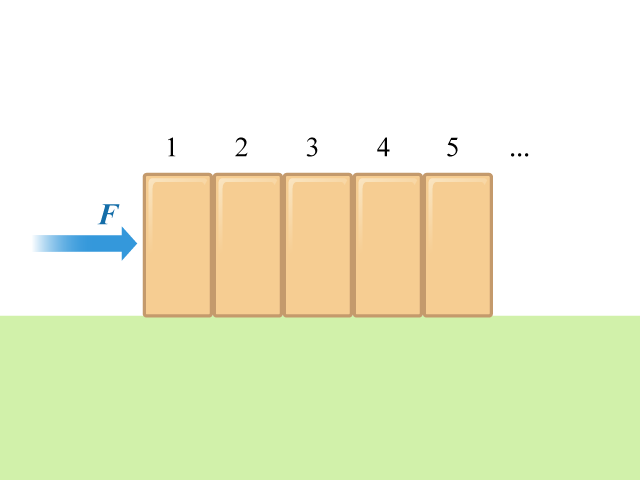
考慮水平面上有 \(100\) 個以直線緊貼排列的方塊,每個方塊的質量等於 \(1.0 \text{ kg}\),如所示。一個 \(F = 100 \text{ N}\) 的力作用於方塊列的左末端,求第 \(60\) 個方塊作用於第 \(61\) 個方塊的力。
你可根據下方指示,先在《方塊列模擬程式》中設定類似的情境,演示方塊列的運動:
【步驟 \(1\)】:計算方塊列的加速度 解題思路
考慮全部 \(100\) 個方塊合併為一個單一的方塊(),作用於合併後方塊的淨力為 \(100 \text{ N}\),應用牛頓第二定律:
\(\begin{align}F &= \left( 1\ \text{kg}\times 100 \right)a \\ 100\ \text{N} &= \left( 100\ \text{kg} \right)a \\ \Rightarrow \ a &= 1\ \text{m}\ {{\text{s}}^{-2}}\end{align}\)
【步驟 \(2\)】:繪畫方塊列的隔離體圖
設 \(f\) 為第 \(60\) 個方塊作用於第 \(61\) 個方塊的力。第 \(61\) 個方塊至 \(100\) 個方塊的隔離體圖,如所示。
【步驟 \(3\)】:計算作用於第 \(61\) 個方塊的力 解題思路
從第 \(61\) 至 \(100\) 的方塊的總質量等於 \(40 \text{ kg}\)。由於方塊列中各方塊的加速度相同,根據牛頓第二定律:
\(\begin{align}f &= m\ a \\ &= \left( 1\ \text{kg}\times 40 \right)\left( 1\ \text{m}\ {{\text{s}}^{-2}} \right) \\ &= 40\ \text{N}\end{align}\)